Repetition Codes
Perhaps the simplest error correcting code is the repetition code.
Repetition Code
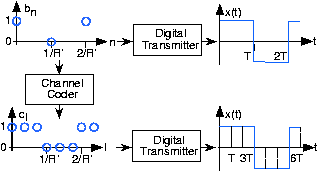
Figure 1. The upper portion depicts the result of directly modulating the bit stream

into a transmitted signal

using a baseband BPSK signal set.

is the datarate produced by the source coder. If that bit stream passes through a (3,1) channel coder to yield the bit stream

, the resulting transmitted signal requires a bit interval

three times smaller than the uncoded version. This reduction in the bit interval means that the transmitted energy/bit decreases by a factor of three, which results in an increased error probability in the receiver.
Here, the transmitter sends the data bit several times, an odd number of times in fact. Because the error probability

is always less than

, we know that more of the bits should be correct rather than in error. Simple majority voting of the received bits (hence the reason for the odd number) determines the transmitted bit more accurately than sending it alone. For example, let's consider the three-fold repetition code: for every bit

emerging from the source coder, the channel coder produces three. Thus, the bit stream emerging from the channel coder

has a data rate three times higher than that of the original bit stream

. The coding table illustrates when errors can be corrected and when they can't by the majority-vote decoder.
| Code | Probability | Bit |
|---|---|---|
| 000 |  | 0 |
| 001 |  | 0 |
| 010 |  | 0 |
| 011 |  | 1 |
| 100 |  | 0 |
| 101 |  | 1 |
| 110 |  | 1 |
| 111 |  | 1 |
Coding Table In this example, the transmitter encodes 00 as 000000. The channel creates an error (changing a 00 into a 11) that with probability

. The first column lists all possible received datawords and the second the probability of each dataword being received. The last column shows the results of the majority-vote decoder. When the decoder produces 00, it successfully corrected the errors introduced by the channel (if there were any; the top row corresponds to the case in which no errors occurred). The error probability of the decoders is the sum of the probabilities when the decoder produces 11.
Thus, if one bit of the three bits is received in error, the receiver can correct the error; if more than one error occurs, the channel decoder announces the bit is 1 instead of transmitted value of 0. Using this repetition code, the probability of

equals

. This probability of a decoding error is always less than

, the uncoded value, so long as

.
Exercise
Demonstrate mathematically that this claim is indeed true. Is

?
This question is equivalent to

or

. Because this is an upward-going parabola, we need only check where its roots are. Using the quadratic formula, we find that they are located at

and

. Consequently in the range

the error rate produced by coding is smaller.
This textbook is open source. Download for free at http://cnx.org/contents/778e36af-4c21-4ef7-9c02-dae860eb7d14@9.72.
Explore CircuitBread

Get the latest tools and tutorials, fresh from the toaster.







