Σ (Sum) and Π (Product) Notation

For reference, this section introduces the terminology used in some texts to describe the minterms and maxterms assigned to a Karnaugh map. Otherwise, there is no new material here.

Σ (sigma) indicates sum and lower case "m" indicates minterms. Σm indicates sum of minterms. The following example is revisited to illustrate our point. Instead of a Boolean equation description of unsimplified logic, we list the minterms.

f(A,B,C,D) = Σ m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15)

or

f(A,B,C,D) = Σ(m₁,m₂,m₃,m₄,m₅,m₇,m₈,m₉,m₁₁,m₁₂,m₁₃,m₁₅)

The numbers indicate cell location, or address, within a Karnaugh map as shown below right. This is certainly a compact means of describing a list of minterms or cells in a K-map.

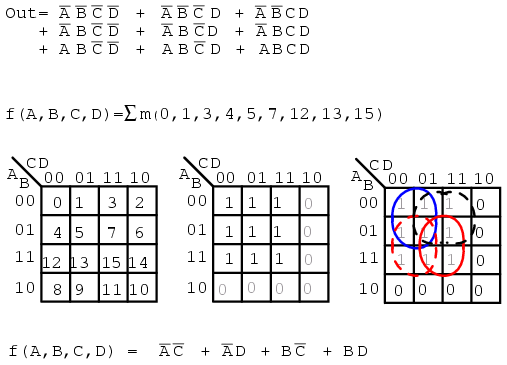
The Sum-Of-Products solution is not affected by the new terminology. The minterms, 1s, in the map have been grouped as usual and a Sum-OF-Products solution written.

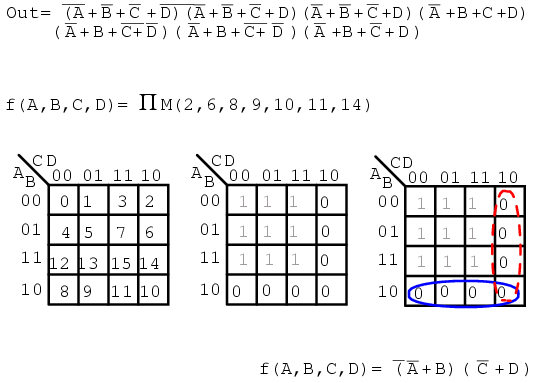
Below, we show the terminology for describing a list of maxterms. Product is indicated by the Greek Π (pi), and upper case "M" indicates maxterms. ΠM indicates product of maxterms. The same example illustrates our point. The Boolean equation description of unsimplified logic, is replaced by a list of maxterms.

f(A,B,C,D) = Π M(2, 6, 8, 9, 10, 11, 14)

or

f(A,B,C,D) = Π(M₂, M₆, M₈, M₉, M₁₀, M₁₁, M₁₄)

Once again, the numbers indicate K-map cell address locations. For maxterms this is the location of 0s, as shown below. A Product-OF-Sums solution is completed in the usual manner.