Electric Potential and Potential Difference
LEARNING OBJECTIVES
By the end of this section, you will be able to:
- Define electric potential, voltage, and potential difference
- Define the electron-volt
- Calculate electric potential and potential difference from potential energy and electric field
- Describe systems in which the electron-volt is a useful unit
- Apply conservation of energy to electric systems
Recall that earlier we defined electric field to be a quantity independent of the test charge in a given system, which would nonetheless allow us to calculate the force that would result on an arbitrary test charge. (The default assumption in the absence of other information is that the test charge is positive.) We briefly defined a field for gravity, but gravity is always attractive, whereas the electric force can be either attractive or repulsive. Therefore, although potential energy is perfectly adequate in a gravitational system, it is convenient to define a quantity that allows us to calculate the work on a charge independent of the magnitude of the charge. Calculating the work directly may be difficult, since

and the direction and magnitude of

can be complex for multiple charges, for odd-shaped objects, and along arbitrary paths. But we do know that because

, the work, and hence

, is proportional to the test charge

. To have a physical quantity that is independent of test charge, we define electric potential

(or simply potential, since electric is understood) to be the potential energy per unit charge:
ELECTRIC POTENTIAL
The electric potential energy per unit charge is

(3.2.1)
Since U is proportional to q, the dependence on q cancels. Thus,

does not depend on

. The change in potential energy

is crucial, so we are concerned with the difference in potential or potential difference

between two points, where

ELECTRIC POTENTIAL DIFFERENCE
The electric potential difference between points

and

,

is defined to be the change in potential energy of a charge

moved from

to

, divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta.

The familiar term voltage is the common name for electric potential difference. Keep in mind that whenever a voltage is quoted, it is understood to be the potential difference between two points. For example, every battery has two terminals, and its voltage is the potential difference between them. More fundamentally, the point you choose to be zero volts is arbitrary. This is analogous to the fact that gravitational potential energy has an arbitrary zero, such as sea level or perhaps a lecture hall floor. It is worthwhile to emphasize the distinction between potential difference and electrical potential energy.
POTENTIAL DIFFERENCE AND ELECTRICAL POTENTIAL ENERGY
The relationship between potential difference (or voltage) and electrical potential energy is given by

(3.2.2)
Voltage is not the same as energy. Voltage is the energy per unit charge. Thus, a motorcycle battery and a car battery can both have the same voltage (more precisely, the same potential difference between battery terminals), yet one stores much more energy than the other because

. The car battery can move more charge than the motorcycle battery, although both are

batteries.
EXAMPLE 3.2.1
Calculating Energy
You have a

motorcycle battery that can move

of charge, and a

car battery that can move

of charge. How much energy does each deliver? (Assume that the numerical value of each charge is accurate to three significant figures.)
Strategy
To say we have a

battery means that its terminals have a

potential difference. When such a battery moves charge, it puts the charge through a potential difference of

, and the charge is given a change in potential energy equal to

. To find the energy output, we multiply the charge moved by the potential difference.
Solution
For the motorcycle battery,

and

. The total energy delivered by the motorcycle battery is

Similarly, for the car battery,

and

Significance
Voltage and energy are related, but they are not the same thing. The voltages of the batteries are identical, but the energy supplied by each is quite different. A car battery has a much larger engine to start than a motorcycle. Note also that as a battery is discharged, some of its energy is used internally and its terminal voltage drops, such as when headlights dim because of a depleted car battery. The energy supplied by the battery is still calculated as in this example, but not all of the energy is available for external use.
CHECK YOUR UNDERSTANDING 3.4
How much energy does a

AAA battery have that can move

?
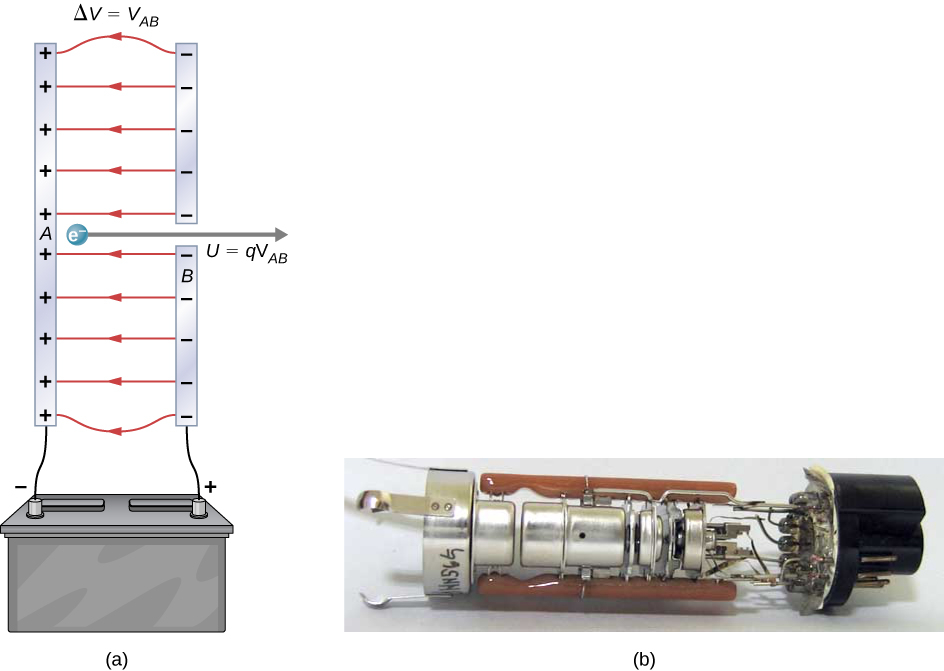
Note that the energies calculated in the previous example are absolute values. The change in potential energy for the battery is negative, since it loses energy. These batteries, like many electrical systems, actually move negative charge—electrons in particular. The batteries repel electrons from their negative terminals (

) through whatever circuitry is involved and attract them to their positive terminals (

), as shown in Figure 3.2.1. The change in potential is

and the charge

is negative, so that

is negative, meaning the potential energy of the battery has decreased when

has moved from

to

(Figure 3.2.1)

EXAMPLE 3.2.2
How Many Electrons Move through a Headlight Each Second?
When a

car battery powers a single

headlight, how many electrons pass through it each second?
Strategy
To find the number of electrons, we must first find the charge that moves in

. The charge moved is related to voltage and energy through the equations

. A

lamp uses

joules per second. Since the battery loses energy, we have

and, since the electrons are going from the negative terminal to the positive, we see that

.
Solution
To find the charge

moved, we solve the equation

:

Entering the values for

and

we get

The number of electrons

is the total charge divided by the charge per electron. That is,

CHECK YOUR UNDERSTANDING 3.5
How many electrons would go through a

lamp?
The Electron-Volt
The energy per electron is very small in macroscopic situations like that in the previous example—a tiny fraction of a joule. But on a submicroscopic scale, such energy per particle (electron, proton, or ion) can be of great importance. For example, even a tiny fraction of a joule can be great enough for these particles to destroy organic molecules and harm living tissue. The particle may do its damage by direct collision, or it may create harmful X-rays, which can also inflict damage. It is useful to have an energy unit related to submicroscopic effects.
Figure 3.2.2 shows a situation related to the definition of such an energy unit. An electron is accelerated between two charged metal plates, as it might be in an old-model television tube or oscilloscope. The electron gains kinetic energy that is later converted into another form—light in the television tube, for example. (Note that in terms of energy, “downhill” for the electron is “uphill” for a positive charge.) Since energy is related to voltage by

, we can think of the joule as a coulomb-volt.
(Figure 3.2.2)



ELECTRON-VOLT
On the submicroscopic scale, it is more convenient to define an energy unit called the electron-volt (eV), which is the energy given to a fundamental charge accelerated through a potential difference of

. In equation form,

An electron accelerated through a potential difference of

is given an energy of

. It follows that an electron accelerated through

gains

. A potential difference of

(

) gives an electron an energy of

(

), and so on. Similarly, an ion with a double positive charge accelerated through

gains

of energy. These simple relationships between accelerating voltage and particle charges make the electron-volt a simple and convenient energy unit in such circumstances.
The electron-volt is commonly employed in submicroscopic processes—chemical valence energies and molecular and nuclear binding energies are among the quantities often expressed in electron-volts. For example, about

of energy is required to break up certain organic molecules. If a proton is accelerated from rest through a potential difference of

, it acquires an energy of

(

) and can break up as many as

of these molecules (

per molecule

molecules). Nuclear decay energies are on the order of

(

) per event and can thus produce significant biological damage.
Conservation of Energy
The total energy of a system is conserved if there is no net addition (or subtraction) due to work or heat transfer. For conservative forces, such as the electrostatic force, conservation of energy states that mechanical energy is a constant.
Mechanical energy is the sum of the kinetic energy and potential energy of a system; that is,

. A loss of

for a charged particle becomes an increase in its

. Conservation of energy is stated in equation form as

or

where

and

stand for initial and final conditions. As we have found many times before, considering energy can give us insights and facilitate problem solving.
EXAMPLE 3.2.3
Electrical Potential Energy Converted into Kinetic Energy
Calculate the final speed of a free electron accelerated from rest through a potential difference of

. (Assume that this numerical value is accurate to three significant figures.)
Strategy
We have a system with only conservative forces. Assuming the electron is accelerated in a vacuum, and neglecting the gravitational force (we will check on this assumption later), all of the electrical potential energy is converted into kinetic energy. We can identify the initial and final forms of energy to be

,

,

,

.
Solution
Conservation of energy states that

Entering the forms identified above, we obtain

We solve this for

:

Entering values for

,

, and

gives

Significance
Note that both the charge and the initial voltage are negative, as in Figure 3.2.2. From the discussion of electric charge and electric field, we know that electrostatic forces on small particles are generally very large compared with the gravitational force. The large final speed confirms that the gravitational force is indeed negligible here. The large speed also indicates how easy it is to accelerate electrons with small voltages because of their very small mass. Voltages much higher than the

in this problem are typically used in electron guns. These higher voltages produce electron speeds so great that effects from special relativity must be taken into account and hence are beyond the scope of this textbook. That is why we consider a low voltage (accurately) in this example.
CHECK YOUR UNDERSTANDING 3.6
How would this example change with a positron? A positron is identical to an electron except the charge is positive.
Voltage and Electric Field
So far, we have explored the relationship between voltage and energy. Now we want to explore the relationship between voltage and electric field. We will start with the general case for a non-uniform

field. Recall that our general formula for the potential energy of a test charge

at point

relative to reference point

is

When we substitute in the definition of electric field (

), this becomes

Applying our definition of potential (

) to this potential energy, we find that, in general,

(3.2.3)
From our previous discussion of the potential energy of a charge in an electric field, the result is independent of the path chosen, and hence we can pick the integral path that is most convenient.
Consider the special case of a positive point charge

at the origin. To calculate the potential caused by

at a distance

from the origin relative to a reference of

at infinity (recall that we did the same for potential energy), let

and

, with

and use

. When we evaluate the integral

for this system, we have

which simplifies to

This result,

is the standard form of the potential of a point charge. This will be explored further in the next section.
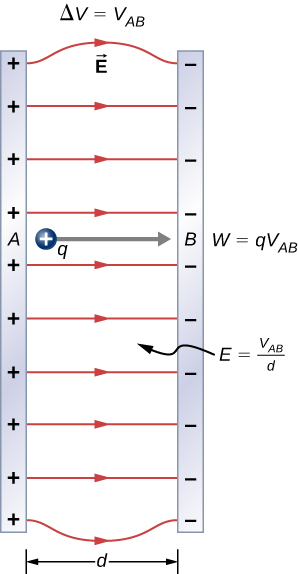
To examine another interesting special case, suppose a uniform electric field

is produced by placing a potential difference (or voltage)

across two parallel metal plates, labeled
(Figure 3.2.3)







From a physicist’s point of view, either

or

can be used to describe any interaction between charges. However,

is a scalar quantity and has no direction, whereas

is a vector quantity, having both magnitude and direction. (Note that the magnitude of the electric field, a scalar quantity, is represented by

.) The relationship between

and

is revealed by calculating the work done by the electric force in moving a charge from point

to point

. But, as noted earlier, arbitrary charge distributions require calculus. We therefore look at a uniform electric field as an interesting special case.
The work done by the electric field in Figure 3.2.3 to move a positive charge

from

, the positive plate, higher potential, to

, the negative plate, lower potential, is

The potential difference between points

and

is

Entering this into the expression for work yields

Work is

; here

, since the path is parallel to the field. Thus,

. Since

, we see that

.
Substituting this expression for work into the previous equation gives

The charge cancels, so we obtain for the voltage between points

and


where

is the distance from

to

, or the distance between the plates in Figure 3.2.3. Note that this equation implies that the units for electric field are volts per meter. We already know the units for electric field are newtons per coulomb; thus, the following relation among units is valid:

Furthermore, we may extend this to the integral form. Substituting Equation 3.2.2 into our definition for the potential difference between points

and

, we obtain

which simplifies to

As a demonstration, from this we may calculate the potential difference between two points (

and

) equidistant from a point charge

at the origin, as shown in Figure 3.2.4.
(Figure 3.2.4)

To do this, we integrate around an arc of the circle of constant radius

between

and

, which means we let

, while using


(3.2.4)
for this system becomes

However,

and therefore

This result, that there is no difference in potential along a constant radius from a point charge, will come in handy when we map potentials.
EXAMPLE 3.2.4
What Is the Highest Voltage Possible between Two Plates?
Dry air can support a maximum electric field strength of about

. Above that value, the field creates enough ionization in the air to make the air a conductor. This allows a discharge or spark that reduces the field. What, then, is the maximum voltage between two parallel conducting plates separated by

of dry air?
Strategy
We are given the maximum electric field

between the plates and the distance

between them. We can use the equation

to calculate the maximum voltage.
Solution
The potential difference or voltage between the plates is

Entering the given values for

and

gives

or

(The answer is quoted to only two digits, since the maximum field strength is approximate.)
Significance
One of the implications of this result is that it takes about

to make a spark jump across a

(

) gap, or

for a

spark. This limits the voltages that can exist between conductors, perhaps on a power transmission line. A smaller voltage can cause a spark if there are spines on the surface, since sharp points have larger field strengths than smooth surfaces. Humid air breaks down at a lower field strength, meaning that a smaller voltage will make a spark jump through humid air. The largest voltages can be built up with static electricity on dry days (Figure 3.2.5).
(Figure 3.2.5)

EXAMPLE 3.2.5
Field and Force inside an Electron Gun
An electron gun (Figure 3.2.2) has parallel plates separated by

and gives electrons

of energy. (a) What is the electric field strength between the plates? (b) What force would this field exert on a piece of plastic with a

charge that gets between the plates?
Strategy
Since the voltage and plate separation are given, the electric field strength can be calculated directly from the expression

. Once we know the electric field strength, we can find the force on a charge by using

. Since the electric field is in only one direction, we can write this equation in terms of the magnitudes,

.
Solution
- The expression for the magnitude of the electric field between two uniform metal plates is
Since the electron is a single charge and is givenof energy, the potential difference must be
. Entering this value for
and the plate separation of
, we obtain
- The magnitude of the force on a charge in an electric field is obtained from the equation
Substituting known values gives
Significance
Note that the units are newtons, since

. Because the electric field is uniform between the plates, the force on the charge is the same no matter where the charge is located between the plates.
EXAMPLE 3.2.6
Calculating Potential of a Point Charge
Given a point charge

at the origin, calculate the potential difference between point

a distance

from

, and

a distance

from

, where the two points have an angle of

between them (Figure 3.2.6).
(Figure 3.2.6)



Strategy
Do this in two steps. The first step is to use

and let

and

, with

and

. Then perform the integral. The second step is to integrate

around an arc of constant radius

, which means we let

with limits

, still using

. Then add the two results together.
Solution
For the first part,

for this system becomes

which computes to

For the second step,

becomes

, but

and therefore

. Adding the two parts together, we get

.
Significance
We have demonstrated the use of the integral form of the potential difference to obtain a numerical result. Notice that, in this particular system, we could have also used the formula for the potential due to a point charge at the two points and simply taken the difference.
CHECK YOUR UNDERSTANDING 3.7
From the examples, how does the energy of a lightning strike vary with the height of the clouds from the ground? Consider the cloud-ground system to be two parallel plates.
Before presenting problems involving electrostatics, we suggest a problem-solving strategy to follow for this topic.
Problem-Solving Strategy: Electrostatics
- Examine the situation to determine if static electricity is involved; this may concern separated stationary charges, the forces among them, and the electric fields they create.
- Identify the system of interest. This includes noting the number, locations, and types of charges involved.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful. Determine whether the Coulomb force is to be considered directly—if so, it may be useful to draw a free-body diagram, using electric field lines.
- Make a list of what is given or can be inferred from the problem as stated (identify the knowns). It is important to distinguish the Coulomb force
from the electric field
, for example.
- Solve the appropriate equation for the quantity to be determined (the unknown) or draw the field lines as requested.
- Examine the answer to see if it is reasonable: Does it make sense? Are units correct and the numbers involved reasonable?
Candela Citations
CC licensed content, Specific attribution
- Download for free at http://cnx.org/contents/7a0f97...; Retrieved from: http://cnx.org/contents/7a0f97...; License: CC BY: Attribution
Introduction to Electricity, Magnetism, and Circuits by Daryl Janzen is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.
Explore CircuitBread

Get the latest tools and tutorials, fresh from the toaster.











