Capacitor Basics: How do Capacitors Work?

Capacitors are an incredibly useful component that are used in a wide variety of circuits for a wide variety of reasons, truly, the variety in applications is nearly mind boggling. In this tutorial, we will learn about what a capacitor is, how to treat a capacitor in a DC circuit, how to treat a capacitor in a transient circuit, how to work with capacitors in an AC circuit, and make an attempt at understanding what is going on with a capacitor at a physics level.

A capacitor is an electrical energy storage device made up of two plates that are as close to each other as possible without touching, which store energy in an electric field. They are usually two-terminal devices and their symbol represents the idea of two plates held closely together.

But in reality, capacitors look nothing like that and even one capacitor to another can look wildly different - ranging from nearly microscopic to the size of a family van.

The storage capacity is measured in capacitance, with the units of Farad, which is related to the amount of charge on the conductive plates versus the voltage between the conductors. If one coulomb of charge yields one volt across the plates, then the capacitor is one farad.

In reality, most capacitors are in the picofarad to millifarad range, though special capacitors can yield much higher capacitances (with other trade-offs in performance).

In a stable DC circuit, with no changes in voltage over a long time, capacitors are extremely simple. You can treat them like they’re not there. In modeling a DC circuit with no transients, you can remove the capacitor and replace it with an open and the circuit will remain exactly the same. An added bonus, if there are any other circuit elements in series with the capacitor, you can ignore them as well. While this can make students in Circuits 1 applaud, this is fairly useless, so let’s look at DC circuits where there is a change in voltage.

In a DC circuit transient, where you’re modeling a switch opening or closing, a capacitor will resist the change in voltage. This resistance is because the current that is flowing into the capacitor is “filling” the capacitor up, it can’t charge or discharge instantaneously. This change in voltage is consistent and can be calculated exactly if you know the capacitance as well as any series resistance. It is modeled with the following equations:

Where:
v_c - voltage across the capacitor
V₁ - input voltage
t - elapsed time since the input voltage was applied
𝜏 - time constant

We’ll go into these types of circuits in more detail in a different tutorial, but at this point, it’s good to look at the equation and see how it reflects the real life behavior of a capacitor charging or discharging. Note specifically the exponential growth and decay and think about why it’s not linear but that the changing slows as the actual voltage gets close to the target voltage.

When discussing how a capacitor works in a DC circuit, you either focus on the steady state scenarios or look at the changes in regards to time. However, with an AC circuit, you generally look at the response of a circuit in regards to the frequency. This is because a capacitor’s impedance isn’t set - it’s dependent on the frequency. This impedance is described by the following equation:

Just as a reminder, omega (ω) = 2π*frequency. Also, j is the electrical engineer’s symbol for the square root of -1, so the representation of the imaginary numbers. With that in mind, let’s look at what this equation means. The j is an imaginary term that helps us understand phase shifts and how much real power we’re getting. We won’t worry about what that means too much now but it’s an important concept we’ll go over ad nauseum when discussing AC circuits. The *omega* is a representation of the frequency that is being applied to the circuit and the ‘c’ is the measured capacitance of the capacitor. As these terms are in the denominator, we can see that if you increase either the frequency or the capacitance, the impedance of the capacitor decreases. If the frequency is 0, the impedance will be infinity (which is why we treat a capacitor as an open in DC circuits) but the impedance will also be 0 if the frequency is infinite.

While I don’t want to bombard you with too many details, I do want to briefly go over a few important points of AC circuits that will be affected by capacitors. This will be repeated in the overview of inductors as they also affect AC circuits. There are two items in particular that I’d like to review and will be the foundational points of AC circuit analysis. These items are in regards to the output voltage compared to the input voltage.

Magnitude: As the impedance of a capacitor changes, it will change the output voltage, making it either larger or smaller, depending on the circuit configuration. This relationship between the output and input voltage is the magnitude and is an important factor to consider.

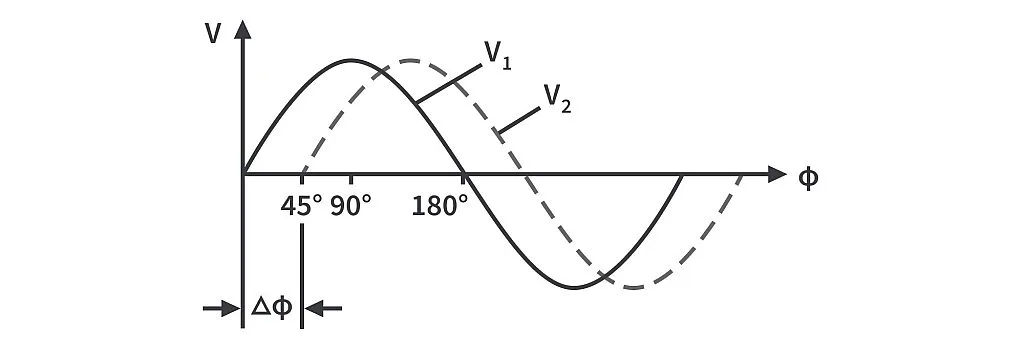
Phase Shift: While magnitude is fairly straightforward, the phase shift can be a little harder to envision. The fact that a capacitor needs some time to charge and discharge means that the shape of the output voltage can be delayed. The amount of delay is considered the phase shift, which may be further confused by the fact that it’s measured in degrees, which is basically a percentage of the full cycle of an alternating signal.

When capacitors are put in series and parallel, they can be combined to simplify calculations and some simulations. It’s very straightforward and if you know how to calculate series and parallel resistors, then there is only one thing to remember. They are the opposite of resistors. With capacitors in parallel, you can simply add the capacitances together. With capacitors in series, you treat them as you do a resistor in parallel, using the following equation.

This can also be simplified in two scenarios. If there are only two capacitors in series, you can use this easier equation:

And if there are only two capacitors in series with the same capacitance, you can simply divide the capacitance by two, making it even easier.

As mentioned previously, a capacitor is made up of two metal plates held close together, separated by a dielectric, which can be practically anything. More often than not, those metal “plates” are actually rolled together like one of those jelly rolls that I learned about watching the British Baking Show, but two pieces, not one.

It’s still easier to imagine, and from a physics point of view is the same, to consider it as two parallel plates. On these plates, as the capacitor is charged up and the voltage across the plates goes up, positive and negative charges will collect on the different plates.

Now, let’s look at the equation that is used to calculate the capacitance of a parallel plate capacitor:

ε is the absolute permittivity of the dielectric between the two plates and I won’t worry about it too much. Just know that if you have a vacuum between the two plates or some different material will affect the overall capacitance. ‘A’ represents the area of the plates - this should make sense as a larger area will yield a larger capacitance. ‘d’ represents the distance between the two plates and shows that the closer the plates are together, the greater the capacitance. This should make sense as, if the plates are closer, the positive and negative charges are more attracted to each other and want to jump through the dielectric to the other plate even more. But they can’t - disregarding quantum effects, no electrons can pass from one plate to another directly. This is why, in a DC circuit when the electrons are flowing in one direction, a capacitor acts as an open. But, then how does current flow in an AC circuit? Let’s discuss that using a metaphor.

I have to confess, I came up with this metaphor and thought I was quite brilliant. Then I saw the Wikipedia page on capacitors and they had nearly the exact same metaphor, so that was a blow to my already fragile ego. Either way, here’s my spin on the water and rubber barrier metaphor.

Remember that, in water/electricity metaphors, water pressure is equivalent to voltage and water flow is equivalent to current. Now imagine a circular pipeline with a reversible pump and a flexible rubber barrier blocking the flow of water. As the pump pushes water consistently in one direction, like a DC voltage, the rubber will stretch and there will be energy stored in that stretch. But, after a certain point, the resistance of the rubber will match the push of the pump, and the movement of water stops. If you flip the direction of the pump, eventually you’ll have the same equilibrium reached the other way. This is akin to a DC voltage charging and discharging a capacitor. So how about AC signals?

If the pump regularly alternates slowly, then the equilibrium will be reached often and water will stop flowing for extended periods of time. However, as the alternations increase in frequency, there will be less time for the rubber barrier to reach its full flex. Eventually, as the pump switches direction quickly enough, it’ll almost be as if the barrier isn’t even there with the water moving back and forth. So, even though no water actually passes through the barrier, the energy passes without any problems. In this way, a capacitor passes AC current, as it’s just the transfer of energy and not an actual physical movement of electrons from one plate to the other.

While we assume that a capacitor works perfectly most of the time, there are some real-life considerations that may or may not be significant enough to need to think about when doing design or troubleshooting. Let’s go over them briefly:

• Equivalent series resistance (ESR). While we assume the capacitor has no resistance, in reality, there is. This is noticeable when the capacitor is charging and discharging in that some power is being dissipated during the process. It also slows down the speed at which a capacitor can charge and discharge.
• Inductance. Usually a much smaller issue than ESR, there is a bit of inductance in any capacitor, which resists changes in current flow. Not a big deal most of the time.
• Voltage limits. Every capacitor has a limit of how much voltage you can put across it before it breaks down. Be careful to give yourself a little extra headspace with the voltage limit to account for any potential voltage spikes.
• Reversed voltages. Some capacitors do not care about voltage polarity but some, particularly electrolytic capacitors, cannot accept reversed voltages or else they’ll explode. Explode may be a strong word, they usually just poof a little and stop working.
• Lifespan. Over time, capacitors age and their capacitance drops. Some technologies struggle with this more than others. For some configurations, this decreased capacitance may not really affect performance but if there’s a tuned circuit dependent on a specific capacitance, this could cause problems.

We’ll go into more depth on the particulars of capacitor uses but wanted to take a moment to discuss their uses at a high level. A few of the most common usages are here below:

• Control AC/DC signal flow. As mentioned previously, a capacitor passes AC signals and blocks DC signals. So if you put a capacitor in series with something, it blocks the DC signal, removing unwanted DC offsets. If you put a capacitor in parallel with something, it shunts AC signals, often this is connected to ground so that you can shunt any unwanted AC signals to ground (like electrical noise).
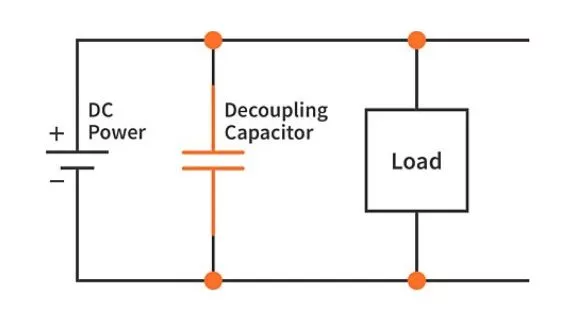
• Smooth power supplies. As capacitors store energy, it is common practice to put a capacitor as close to a load (something that consumes power) so that if there is a voltage dip on the line, the capacitor can provide short bursts of current to resist that voltage dip.
• Tuning resonant frequencies. For electromagnetic systems, antennas, and transmission lines, the capacitance of the system affects what frequency things resonate at.
• Phase shift correction. If you’re not familiar with AC circuits, this won’t make much sense but if a load is too inductive, it can reduce the efficiency of a system. To counteract this, you can add capacitance to the load.

Capacitors are incredibly simple in their concept but the details, the way they work with DC and AC signals, and their imperfections provide an unbelievably diverse amount of applications and considerations. Dozens of tutorials can be written about the different capacitor uses and we’ll see how many of them we’re able to put together. If you have any questions, feel free to leave a comment below or jump on our Discord channel to ask!