Delta-Wye Transformation

Most of the time, resistor networks can be easily simplified by combining the series and parallel arrangement of resistors. But sometimes the resistors are neither in series nor in a parallel combination. Let’s consider the below network:

If we are asked to find the equivalent resistance between terminals A and B, how do we start simplifying the network? Can you find a way to reduce this network using the series-parallel combination of resistors? The answer is no. It isn’t straightforward because the resistors are neither in series nor in a parallel configuration. This is a situation where we can make use of the ‘Delta-Wye’ (Δ-Y) transformation.

The name ‘Delta-Wye’ comes from the arrangement of resistors such that they resemble the shape ‘Δ’ and ‘Y’. At times, the ‘Y’ configuration can be referred to as the “star” configuration. Their drawing style emphasizes that these are 3-terminal configurations.

The ‘Δ-Y’ resistor networks can also be redrawn as ‘𝛑-T’ networks, which are shown in the image below. They are the exact same networks, only with a different drawing style.

We can transform a Δ configuration of resistors to a Y configuration, and the other way around using a set of transformation equations. This transformation is to convert the network into a form that is relatively easier to simplify. We won't be discussing how the transformation equations are derived. Instead, we’ll be looking at some interesting examples which can give you an idea about when and how to make use of the Δ-Y transformation to solve a seemingly complicated network. Let’s take a look at the transformation equations where R₁, R₂, and R₃ are the resistors of the Y network, and R_A, R_B, and R_C are the resistors of the Δ network.

Note: These transformation equations also hold true for the ‘𝛑-T’ resistor networks.

These equations are the formulae that the CircuitBread Delta-Wye calculator is based on and that calculator can be used to make the process of converting between the two forms faster, easier, and less likely to have errors in the process.

Example 1:

We’ll start with a really basic problem. Below is a Δ network and we need to convert it to a Y network. We’ll use the above equations directly to convert the network.

The first step should always be to identify and label the resistors in the network.

Once we have our resistors labeled, the next step involves a little bit of visualization. It’s always a good practice to imagine what the converted network would look like before blindly putting in the values in the transformation equation. Something like overlapping the Δ and Y network and getting an intermediate network.

You won't actually need to draw this intermediate network anywhere, it is just to avoid any confusion regarding the position of resistors.

Now we can use the Δ → Y transformation equations to obtain the values of R₁, R₂, and R₃

So we get the equivalent star network as

Awesome! We've got a Y equivalent of our Δ network. You can actually convert this network back to the original Δ network using the Y → Δ transformation equations.

Example 2:

In this example, we need to find the equivalent resistance between the terminals A and B. That means we need to reduce the given arrangement of resistors to a single resistor.

We can see that there’s a Δ structure on the outside and a Y structure on the inside of this resistor network. We can begin by converting the inner Y network to its Δ equivalent.

The Y network on the inside has all the resistors having a value of 3Ω.

The intermediate network would look something like the below figure.

Now we can simply put these values of resistors in our Y → Δ conversion formula to get R_A, R_B, and R_C.

Aha! We’ve got the values of all the three Δ resistors of the network as the same, 9Ω. An interesting and rather useful conclusion from the values obtained above is that, if you have a Y network with all the resistors having the same value, you can simply multiply them by 3 and get the resistor values of its Δ equivalent! And similarly, if all the resistors of a Δ network have the same value, you can divide them by 3 and get the resistor values of its Y equivalent circuit.

So now our updated network after the Y → Δ transformation looks something like this:

We can see that the resistors of the Δ network that we’ve just obtained are in a parallel arrangement with the resistors of the outer Δ network of our original circuit. We’ve already discussed in great detail how we can solve series and parallel combinations of resistors to simplify a network. So let's do it:

Because we need to find the resistance between the terminals A and B, the 6Ω resistors present between AC and CB can be considered in series and this circuit can be further modified as:

Finally, solving this parallel combination of resistors will give us the equivalent resistance between A and B,

Example 3:

Finally, we have the network we saw at the beginning of this tutorial. Now that we know about the Δ → Y conversion, we can make use of it to find the equivalent resistance between the terminals A and B.

The above network consists of two Δ networks. Let’s take the upper Δ arrangement of resistors and convert it to its Y equivalent using the Δ → Y conversion formula.

Once again, we’ll start with labeling the resistors to ease the process.

Our intermediate network will look something like this:

With these numbers and the proper assignment of where the resistors go, can you calculate this or even use our Delta-Wye calculator to get the answer yourself? Try it and then expand the answer below to see if you get the right answer!

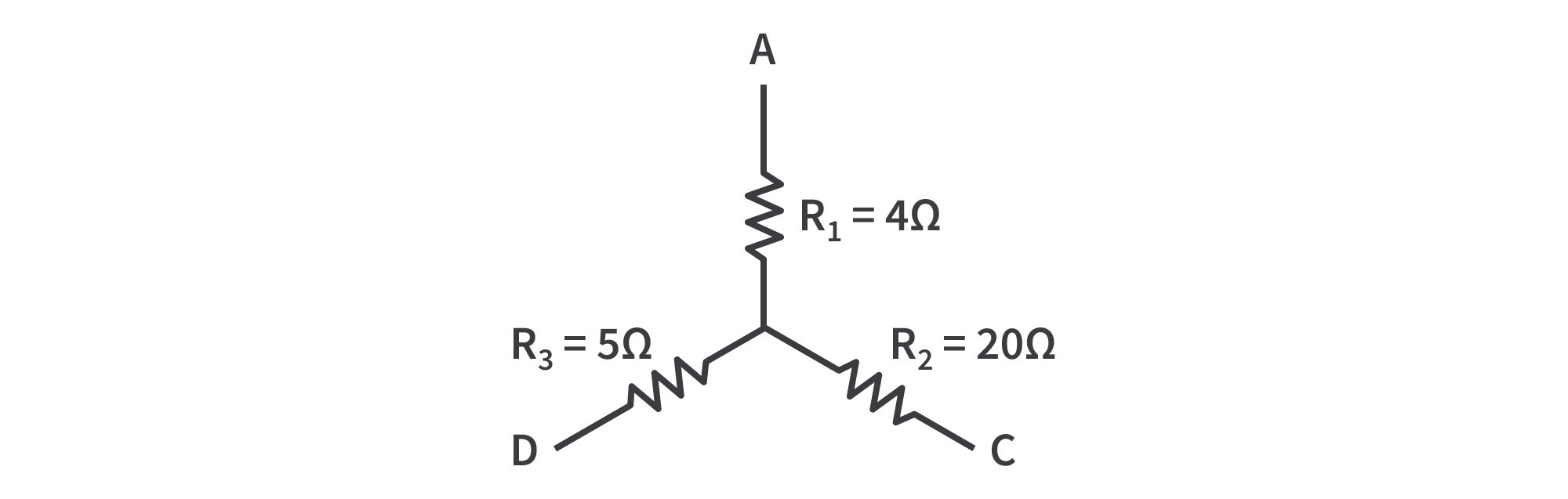
Now that we have the Y equivalent of the Δ network, we can replace this in our original circuit.

The updated network looks something like this. Once again, we are left with a series and parallel combination of resistors. Moving forward from here is pretty easy.

This is how Δ - Y transformation helps us. It always converts the network into a form that can be easily solved further using the basic network reduction techniques.