Norton Theorem - Finding a Norton Equivalent Circuit
Published
Similar to Thévenin's Theorem, there is a way to simplify a circuit and represent it with only two components. Unlike Thévenin's Theorem, Norton’s Theorem uses a current supply and resistor in parallel, versus a voltage supply and a resistor in series.

Simplifying a circuit yields several benefits - if you need to iterate loads, the calculations are significantly simpler and you can maximize power transfer as you can see the impedance your load sees. In our experience here at CircuitBread, Thévenin's Theorem is used more often than Norton’s, but it’s important to know about Norton’s as well.
In this tutorial, let’s go over the steps you should follow to create a Norton equivalent circuit and then go through two examples to show those steps in action.
Step by Step:
- Review your circuit, familiarize yourself, identify your load and the nodes it is hooked to.
- Remove the load resistor and replace it with a short circuit.
- Find INorton by calculating the current through the short circuit where the load was.
- Find RNorton by creating an open circuit where the load resistor is, shorting all voltage sources and by open circuiting all the current sources. Once this is done, calculate the resistance seen by the open circuit.
- Replace load and find the current flowing through the load or voltage across the load with these new values.
- Sanity check!
The steps are quite straightforward but let’s do some examples to make sure we understand their details.
Example #1
#1. Review your circuit, familiarize yourself, identify your load and the nodes it is hooked to.
Let’s start with this first example:

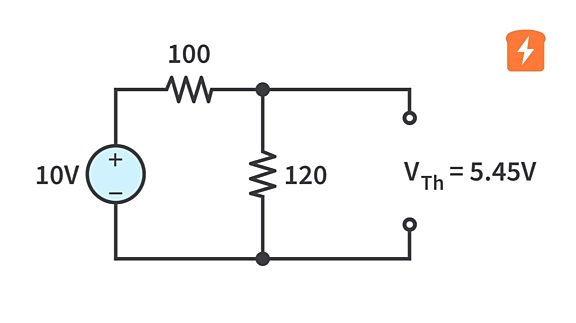
We take a moment to look at this circuit, identify the load resistor, note it has a voltage source (which we’ll care about later), and we see that our load is in series with a 200Ω resistor, which is then in parallel with a 500Ω resistor, all of which is in series with a 50Ω resistor. Without doing any math, we can see the flow of the current and roughly estimate that the total current flowing out of that voltage source should be in the tens of milliamps. Okay, now we’re familiar with the circuit and have a rough idea of what to expect. Let’s move on!
#2. Remove the load resistor and replace it with a short circuit.
As we know where the nodes are for the load resistor, remove the resistor and short circuit those nodes.

This is a straightforward step and no calculations are needed, though it is tied tightly to the third step.
#3. Find INorton by calculating the current through the short circuit where the load was.
Using the circuit diagram we created in step 2, we now solve for the current through the short circuit where the resistor was. This won’t require either of Kirchoff’s Laws, we can simply find the equivalent resistance, find out the total current created by the voltage source, and then find out how much current is going through the 200Ω.
Equivalent resistance for all resistors = 192.857Ω
Itotal = 51.85 mA
Voltage drop over 50Ω resistor = 2.59V
V2 = 10 - 2.59 = 7.41V
INorton = 7.41V / 200Ω = 37.05mA
#4. Find RNorton by creating an open circuit where the load resistor is, shorting all voltage sources and by open circuiting all the current sources. Once this is done, calculate the resistance seen by the open circuit.
The first step is to redraw the circuit as indicated. Since the voltage source goes to a short-circuit and the load resistor becomes an open, you should get the following circuit:

We then have the 50Ω and 500Ω resistors in parallel that are then in series with the 200Ω resistor. This gives us 245.4545Ω looking back into the circuit, which is RNorton.
#5. Replace load and find the current flowing through the load or voltage across the load with these new values.
In this step, we just put together the Norton circuit, as seen in the image below.

You not only have the current source and the Norton resistor in parallel, you put the load back in. This is the final product of the transformation and now you’re done! Or are you?
#6. Sanity check! Is the current through or voltage across the load the same before and after the transformation? If you can’t compare those via calculation or SPICE simulation, do the values seem reasonable intuitively? Are the polarities correct? We knew that the current was going to be in the tens of milliamps and the resistance seems right. The easiest way to confirm is via a SPICE simulation, though the best when learning circuits is just to solve the circuits both before and afterward. For now, we’ll have the SPICE simulation comparing them.

The numbers are close enough, accounting for rounding errors, and it looks good! We’re now ready to jump into the second example.
Example #2

For this second example, we have a slightly more complicated circuit. But I think the results may surprise you. Let’s get started!
#1. Review your circuit, familiarize yourself, identify your load and the nodes it is hooked to.
We see that we have two power sources in this circuit, a voltage and current source and have moved the resistors around a bit from the previous example. But we can look at it and know by inspection that the current through the 200Ω is completely controlled by the current source but that the voltage across the 400Ω resistor, and the 100Ω and 50Ω resistors in series, is 5V.
#2. Remove the load resistor and replace it with a short circuit.

Now we have the circuit with the load resistor removed and a short circuit in its place. Make sure you both verify the nodes are connected properly and I sometimes leave little dots at those nodes to make sure I don’t forget where the load resistor was.
#3. Find INorton by calculating the current through the short circuit where the load was.
Calculate the current through the short circuit. Since the 100Ω resistor is in series with the load resistor, the current is simply 5V/100Ω = 50mA. Thus, our INorton is 50mA. Very straightforward!
#4. Find RNorton by creating an open circuit where the load resistor is, shorting all voltage sources and by open circuiting all the current sources. Once this is done, calculate the resistance seen by the open circuit.

By opening up the current source and shorting the voltage source, the circuit is greatly simplified. And, if you notice, the removal of the current source doesn’t even affect anything, as the shorted voltage source makes everything but the 100Ω resistor unimportant. And you can see that the 100Ω resistor is our RNorton.
#5. Replace load and find the current flowing through the load or voltage across the load with these new values.

We create our new Norton Equivalent Circuit and put the load back in, now doing our calculations if necessary.
#6. Sanity check! It’s at this point we realize that, even though our first glance made it seem like this example would be harder, this was actually much easier to do! The current source and two of the resistors are made unimportant because of the location of the voltage source. We do the LTSpice simulation just because we can and can see that, since we don’t have any rounding errors on this example, the current through the load is the exact same. Success!

Summary
Norton’s Theorem is pretty straightforward if you remember all the steps. There’s no magic and, really, the end result should just make sense once you’re done. As the steps are simple but also easy to forget, we made this little image that goes through the steps quickly that you can use as a reminder when necessary.

Get the latest tools and tutorials, fresh from the toaster.