What is Electric Potential? | Explanation and Examples

Published Jul 05, 2024

This tutorial is all about the energy associated with electrical interactions. Every time you turn on a light or use an electronic device, you are using electrical energy, an indispensable component of our technological society. Using work and energy concepts makes it easier to solve a variety of problems in electricity. In circuits, a difference in potential from one point to another is often called voltage. Potential and voltage are crucial to understanding how electric circuits work and have equally important applications in many devices.

Electric Potential Energy

Electric field exerts force on a charged particle ( $F = qE$ ) which can do work. This work can be expressed in terms of electric potential energy which is dependent on the position of the charged particle in the electric field; just as gravitational potential energy depends on the distance of a mass from the earth’s surface.

When a force $\overrightarrow{F}$ acts on a particle that moves from point a to point b, the work done by the force is given by

$W_{a \rightarrow b} = \int_{a}^{b} \overrightarrow{F} \hspace{0.1cm} \cdot \hspace{0.1cm} d\overrightarrow{l} = \int_{a}^{b} F \hspace{0.1cm} cos\o \hspace{0.1cm} dl$

(1)

where $dl$ is an infinitesimal displacement along the particle’s path and $\o$ is the angle between $\overrightarrow{F}$ and $dl$ at each point along the path. If $\overrightarrow{F}$ is conservative, the work done by $\overrightarrow{F}$ can be expressed in terms of potential energy $U$ . When the particle moves from a point where the potential energy is $U_{a}$ to a point where it is $U_{b}$ , the change in potential energy is $\Delta U = U_{b} - U_{a}$ and the work done by the force is

$W_{a \rightarrow b} = U_{a} - U_{b} = -\Delta U$

(2)

$U_{a}$ is the potential energy at the initial position and $U_{b}$ is the potential energy at final position. When $U_{a}$ is greater than $U_{b}$ , the force does positive work on the particle as it “falls” from a point of higher potential energy (a) to a point of lower potential energy (b); the potential energy decreases. When a tossed ball is moving upward, the gravitational force does negative work during the ascent as the potential energy increases. When the ball starts falling, gravity does positive work, and the potential energy decreases. The force does positive work if the net displacement of the particle is in the same direction as the force.

Electric Potential Energy in a Uniform Field

For an electric field that exerts a force $\overrightarrow{F} = qE$ ,

$W_{a \rightarrow b} = Fd = qEd$

(3)

Consider a positive test charge $q_{0}$ moving in a uniform electric field.

pos charge moving in and moving opposite

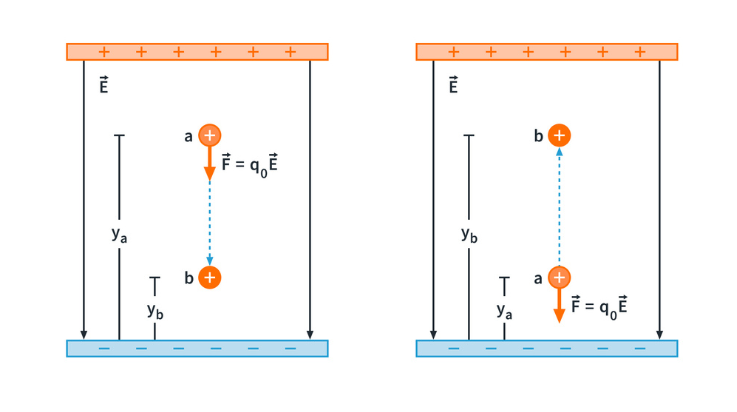
Figure 1: A positive charge moving (a) in the direction of $\overrightarrow{E}$ and (b) in the direction opposite $\overrightarrow{E}$

For Fig.1 (a), the field does positive work on the test charge because the force (pointing down) is in the same direction as the net displacement of the test charge. Since $W_{a \rightarrow b} = - \Delta U$ , if the work is positive then the potential energy ( $U$ ) decreases. For Fig.1 (b), the field does negative work on the charge and the potential energy increases.

Consider a negative test charge $q_{0}$ moving in a uniform electric field. Recall that when $q$ is negative, the force is opposite the field direction.

Negative charge moving in and the opposite

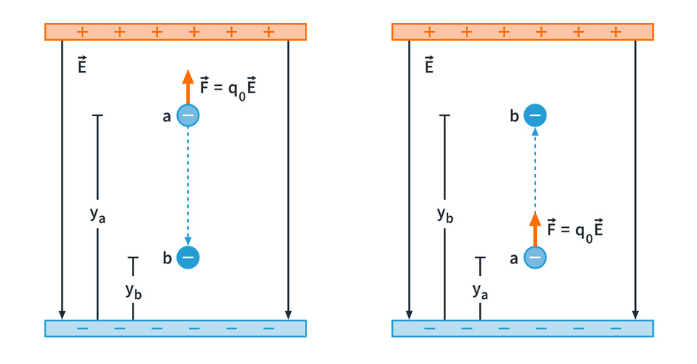
Figure 2: A negative charge moving (a) in the direction of $\overrightarrow{E}$ and (b) in the direction opposite $\overrightarrow{E}$

For Fig.2 (a), the work is negative since the force (pointing upward) is in the opposite direction as the net displacement of the negative test charge and the potential energy increases. For Fig.2 (b), the work is positive, and the potential energy decreases.

This shows us that whether the test charge is positive or negative, the following general rules apply:

$U$ decreases if $q_{0}$ moves in the same direction as the electric force $\overrightarrow{F} = q_{0} E$
$U$ increases if $q_{0}$ moves in the opposite direction as the electric force $\overrightarrow{F} = q_{0} E$

This is the same behavior as for gravitational potential energy, which increases if a mass m moves upward (opposite the direction of the gravitational force $\overrightarrow{F}_{g}$ ) and decreases if m moves downward (in the direction of $\overrightarrow{F}_{g}$ ).

When $U$ increases: An alternative but equivalent viewpoint is to consider how much work we would have to do to “raise” a particle from a point b where the potential energy is $U_{b}$ to a point a where it has a greater value $U_{a}$ (pushing two positive charges closer together, for example). To move the particle, we need to exert an additional external force $\overrightarrow{F}_{ext}$ that is equal and opposite to the electric-field force and does positive work. Therefore, the potential energy difference $U_{a} - U_{b}$ is the work that must be done by an external force to move the particle from b to a, overcoming the electric force. This viewpoint also works if $U_{a}$ is less than $U_{b}$ ; an example is moving two positive charges away from each other. In this case, $U_{a} - U_{b}$ is still equal to the work done by the force, but now the work is negative.

Electric Potential Energy of Point Charges

The idea of electric potential energy isn’t restricted to a uniform electric field. We can apply this concept to a point charge in any electric field caused by a static charge distribution. Recall that we can represent any charge distribution as a collection of point charges. It is therefore useful to calculate the work done on one test charge $q_{0}$ moving in the field caused by a stationary point charge $q$ .

Figure 3: Test charge $q_{0}$ moves from a to b along a straight line extending radially from charge $q$ .

Note that the work done on $q_{0}$ by the electric field of $q$ does not depend on the path taken, but only on the distances $r_{a}$ and $r_{b}$ .

The force on $q_{0}$ is given by Coulomb’s law,

$\setcounter{equation}{3} \begin{equation}\groupequation{ \begin{split} F_{r} = \frac{1}{4\pi \epsilon _{0}} \frac{qq_{0}}{r^{2}} \end{split} }\end{equation} \end{document}$

If $q$ and $q_{0}$ have the same sign, the force is repulsive while if they have opposite signs, the force is attractive. The force is not constant during the displacement, and we must integrate to calculate the work Wab done on $q_{0}$ by Fr as $q_{0}$ moves from a to b:

$\setcounter{equation}{4} \begin{equation}\groupequation{ \begin{split} W_{a \rightarrow b} & = \int_{r_{a}}^{r_{b}} F_{r} \hspace{0.1cm} dr = \int_{r_{a}}^{r_{b}} \frac{1}{4\pi \epsilon _{0}} \frac{qq_{0}}{r^{2}} \hspace{0.1cm} dr \\ & = \frac{qq_{0}}{4\pi \epsilon _{0}} \left ( \frac{1}{r_{a}} -\frac{1}{r_{b}}\right ) \end{split} }\end{equation} \end{document}$

This is also valid for general displacements a to b that do not lie on the same radial line. The work done depends only on $r_{a}$ and $r_{b}$ , not on the details of the path. If $q_{0}$ returns to its starting point a by a different path, the total work done is zero. These are the qualities of a conservative force. Thus, the force on $q_{0}$ is a conservative force.

The result of the integral is consistent with $W_{a \rightarrow b} = U_{a} - U_{b} = - \Delta U$ if we define the potential energy at a and b to be

$U_{a} = qq_{0} / 4\pi \epsilon _{0} r_{a}$ when $q_{0}$ is a distance $r_{a}$ from $q$
$U_{b} = qq_{0} / 4 \pi \epsilon _{0} r_{b}$ when $q_{0}$ is a distance $r_{b}$ from $q$

Thus, the electric potential energy of two point charges is

$\setcounter{equation}{5} \begin{equation}\groupequation{ \begin{split} U = \frac{1}{4\pi \epsilon _{0}} \frac{qq_{0}}{r} \end{split} }\end{equation} \end{document}$

where $r$ is the distance between the two charges. The potential energy is positive if the charges have the same sign and negative if they have opposite signs.

Potential energy is defined relative to a chosen reference point where $U = 0$ is assigned. In eq.(6), $U$ is zero when $q$ and $q_{0}$ are infinitely far apart ( $r = \infty$ ). Therefore $U$ represents the work that would be done on the test charge $q_{0}$ by the field of $q$ if $q_{0}$ moved from an initial distance r to infinity. If $q$ and $q_{0}$ have the same sign, the interaction is repulsive in that they will repel each other, the work is positive, and $U$ is positive at any finite separation. As r approaches infinity, $U$ decreases and approaches zero. If $q$ and $q_{0}$ have opposite signs, the interaction is attractive, the work done is negative, and $U$ is negative. As r approaches infinity, $U$ increases and approaches zero.

We emphasize that the potential energy $U$ given by eq.(6) is a shared property of the two charges. If the distance between $q$ and $q_{0}$ is changed from $r_{a}$ to $r_{b}$ , the change in potential energy is the same whether $q$ is held fixed and $q_{0}$ is moved or $q_{0}$ is held fixed and $q$ is moved. For this reason, we never use the phrase “the electric potential energy of a point charge.” Likewise, if a mass m is at a height h above the earth’s surface, the gravitational potential energy is a shared property of the mass m and the earth.

Suppose the electric field in which the charge $q_{0}$ moves is caused by several point charges $q_{1}$ , $q_{2}$ , $q_{3}$ , ... at distances $r_{1}$ , $r_{2}$ , $r_{3}$ from $q_{0}$ .

Figure 4: The potential energy associated with a charge $q_{0}$ at point a depends on the other charges $q_{1}$ , $q_{2}$ , and $q_{3}$ and on their distances $r_{1}$ , $r_{2}$ and $r_{3}$ from point $a$ .

The total work done on $q_{0}$ given there is some displacement is the sum of the contributions from the individual charges. The potential energy associated with the test charge $q_{0}$ at point $a$ in Fig. 4 is the algebraic sum (not a vector sum)

$\setcounter{equation}{6} \begin{equation}\groupequation{ \begin{split} U = \frac{q_{0}}{4\pi \epsilon _{0}} \left ( \frac{q_{1}}{r_{1}} + \frac{q_{2}}{r_{2}} + \frac{q_{3}}{r_{3}} + \cdots \right ) = \frac{q_{0}}{4\pi \epsilon _{0}} \sum_{i} \frac{q_{i}}{r_{i}} \end{split} }\end{equation} \end{document}$

Electric Potential

Electric potential is the electric potential energy per unit charge. The potential $V$ is defined at any point in an electric field as the potential energy $U$ per unit charge associated with a test charge $q_{0}$ at that point:

$\setcounter{equation}{7} \begin{equation}\groupequation{ \begin{split} V = \frac{U}{q_{0}} \end{split} }\end{equation} \end{document}$

Potential energy and charge are both scalars, so the potential is a scalar. Its unit is energy divided by charge. The SI unit of potential, called the volt (V) in honor of the Italian physicist Alessandro Volta (1745–1827), is equal to 1 Joule per Coulomb:

$1V = 1 \hspace{0.1cm} J/C$

Let’s put eq. (2), which relates the work done by the electric force during a displacement from $a$ to $b$ to the quantity $- \Delta U = - \left ( U_{b} - U_{a} \right )$ , on a “work per unit charge” basis. Dividing this equation by $q_{0}$ and substituting eq. (8), we obtain

$\setcounter{equation}{8} \begin{equation}\groupequation{ \begin{split} \frac{W_{a \rightarrow b}}{q_{0}} = - \frac{\Delta U}{q_{0}} &= - \left ( \frac{U_{b}}{q_{0}} - \frac{U_{a}}{q_{0}} \right ) \\ &= - \left ( V_{b} - V_{a}\right ) \\ &= V_{a} - V_{b} \end{split} }\end{equation} \end{document}$

We call $V_{a}$ and $V_{b}$ the potential at point $a$ and $b$ , respectively. Thus the work done per unit charge by the electric force when a charged body moves from $a$ to $b$ is equal to the potential at $a$ minus the potential at $b$ .

The difference $V_{a} - V_{b}$ is called the potential of $a$ with respect to $b$ ; we abbreviate this difference as $V_{ab} = V_{a} - V_{b}$ . This is often referred to as the potential difference between $a$ and $b$ . However this is ambiguous unless the reference point is specified. In electric circuits, the potential difference between two points is called the voltage. Eq. (9) then states that $V_{ab}$ , the potential(in V) of a with respect to b, equals the work done (in J) by the electric force when a unit charge (1 C) moves from $a$ to $b$ OR $V_{ab}$ , the potential of $a$ with respect to $b$ , equals the work that must be done by an external force to move a unit charge slowly from $a$ to $b$ against the electric force.

To find the potential V due to a single point charge, we substitute eq.(6) to eq.(8)

$\setcounter{equation}{9} \begin{equation}\groupequation{ \begin{split} V = \frac{U}{q_{0}} = \frac{1}{4\pi \epsilon _{0}} \frac{q}{r} \end{split} }\end{equation} \end{document}$

where $r$ is the distance from the point charge $q$ to the point at which the potential is evaluated. If $q$ is positive, the potential that it produces is positive at all points; if $q$ is negative, it produces a potential that is negative at all points. Both potential and electric field are independent of the test charge $q_{0}$ used to define them.

The potential due to a collection of point charges is given by

$\setcounter{equation}{10} \begin{equation}\groupequation{ \begin{split} V = \frac{U}{q_{0}} = \frac{1}{4\pi \epsilon _{0}} \sum_{i} \frac{q_{i}}{r_{i}} \end{split} }\end{equation} \end{document}$

The electric potential due to a collection of point charges is the scalar sum of the potentials due to each charge.

When we have a continuous distribution of charge along a line, over a surface, or through a volume, we divide the charge into elements, and the sum becomes an integral:

$\setcounter{equation}{11} \begin{equation}\groupequation{ \begin{split} V = \frac{1}{4\pi \epsilon _{0}} \int \frac{dq}{r} \end{split} }\end{equation} \end{document}$

The potential defined by eqs. (11) and (12) is zero at points that are infinitely far away from all the charges.

The electric potential at a certain point is the potential energy that would be associated with a unit charge placed at that point. This is why potential is measured in Volts, or Joules per Coulomb. Take into account, too, that a charge does not have to be at a given point for a potential $V$ to exist at that point. (In the same way, an electric field can exist at a given point even if there’s no charge there to respond to it.)

Electric Potential from Electric Field

In some problems in which the electric field is known or can be found easily, it is easier to determine $V$ from $\overrightarrow{E}$ . The force on a test charge $q_{0}$ can be written as $\overrightarrow{F} = q_{0} E$ so from eq. (1), as the test charge moves from $a$ to $b$ , the work done by the electric force is given by

$\setcounter{equation}{12} \begin{equation}\groupequation{ \begin{split} W_{a\rightarrow b} = \int_{a}^{b} \overrightarrow{F} \cdot d\overrightarrow{l} = \int_{a}^{b} q_{0}\overrightarrow{E} \cdot d\overrightarrow{l} \end{split} }\end{equation} \end{document}$

If we divide this by $q_{0}$ and compare the result with eq. (9), we find

$\setcounter{equation}{13} \begin{equation}\groupequation{ \begin{split} V_{a} - V_{b} = \int_{a}^{b} \overrightarrow{E} \cdot d\overrightarrow{l} = \int_{a}^{b} E \hspace{0.1cm} cos\o \hspace{0.1cm} dl \end{split} }\end{equation} \end{document}$

where is the angle between $\overrightarrow{E}$ and $d\overrightarrow{l}$ . The value of $V_{a} - V_{b}$ is independent of the path taken from $a$ to $b$ , just as the value of $W_{a\rightarrow b}$ is independent of the path. To interpret eq. (14), remember that $\overrightarrow{E}$ is the electric force per unit charge on a test charge. If the line integral $\int_{a}^{b} \overrightarrow{E} \cdot d\overrightarrow{l}$ is positive, the electric field does positive work on a positive test charge as it moves from $a$ to $b$ . In this case the electric potential energy decreases as the test charge moves, so the potential energy per unit charge decreases as well; hence $V_{b} < V_{a}$ and $V_{a} - V_{b}$ is positive. Eq. (14) can be rewritten as

$\setcounter{equation}{14} \begin{equation}\groupequation{ \begin{split} V_{a} - V_{b} = - \int_{b}^{a} \overrightarrow{E} \cdot d\overrightarrow{l} \end{split} }\end{equation} \end{document}$

This is when the limits are reversed and it has a slightly different interpretation. To move a unit charge slowly against the electric force, we must apply an external force per unit charge equal to $- \overrightarrow{E}$ , equal and opposite to the electric force per unit charge $\overrightarrow{E}$ . Eq.(15) says that the potential of a with respect to b equals the work done per unit charge by this external force to move a unit charge from $b$ to $a$ . This is the same alternative interpretation we discussed under eq.(9).

Both eq. (14) and (15) also show that the unit of potential difference (1 V) is equal to the unit of electric field (1 N/C) multiplied by the unit of distance (1 m). Hence the unit of electric field can be expressed as 1 volt per meter (1 V/m) as well as (1 N/C). In practice, the volt per meter is typically the unit of electric field magnitude.

Electron Volts

The magnitude $e$ of the electron charge can be used to define a unit of energy that is useful in many calculations with atomic and nuclear systems. When a particle with charge $q$ moves from a point with potential $V_{b}$ to a point with potential $V_{a}$ , the change in the potential energy $U$ is

$U_{a} - U_{b} = q\left ( V_{a} - V_{b} \right ) = qV_{ab}$

If charge $q$ equals the magnitude $e$ of the electron charge, $1.602 \times 10^{-19}$ C, and the potential difference is $V_{ab} = 1 \hspace{0.1cm} V = 1 \hspace{0.1cm} J/C$ , the change in energy is

$U_{a} - U_{b} = \left ( 1.602 \times 10^{-19} \hspace{0.1cm} C\right )\left ( 1 \hspace{0.1cm} J/C \right ) = 1.602 \times 10^{-19} \hspace{0.1cm} J$

This energy quantify is defined to be 1 electron volt (1 eV):

$1 \hspace{0.1cm} eV = 1.602 \times 10^{-19} \hspace{0.1cm} J$

Example 1: A proton ( $e = + 1.602 \times 10^{-19} \hspace{0.1cm} C$ ) moves a distance $d = 0.50 \hspace{0.1cm} m$ in a straight line between points $a$ and $b$ in a linear accelerator. The electric field is uniform along this line, with magnitude $E = 1.5 \times 10^{7} \hspace{0.1cm} V/m$ in the direction from $a$ and $b$ .

Determine
(a) the force on the proton
(b) the work done on the proton by the field
(c) the potential difference $V_{a} - V_{b}$

Solution
This problem uses the relationship between electric field and electric force. It also uses the relationship between force, work, and potential energy difference. We are given the electric field, so we can conveniently find the electric force on the proton. $\overrightarrow{E}$ is also uniform and so the force on the proton is constant. This means that solving for the work is straightforward. Once the work is known, we find $V_{a} - V_{b}$ using eq. (9).

(a) The force on the proton is in the same direction as the electric field, and its magnitude is

$\begin{aligned} F & = qE = \left ( 1.602 \times 10^{-19} \hspace{0.1cm} C \right ) \left ( 1.5 \times 10^{7} \hspace{0.1cm} N/C \right ) \\ & = \[ \boxed{2.4 \times 10^{-12} \hspace{0.1cm} N}\] \end{aligned}$

(b) The force is constant and in the same direction as the displacement, so the work done on the proton is

$\begin{aligned} W_{a \rightarrow b} & = Fd = \left ( 2.4 \times 10^{-12} \hspace{0.1cm} N \right )\left ( 0.50 \hspace{0.1cm} m \right ) = 1.2 \times 10^{-12} \hspace{0.1cm} J \\ & = \left ( 1.2 \times 10^{-12} \hspace{0.1cm} J \right ) \frac{1 \hspace{0.1cm} eV}{\underset{conversion \hspace{0.1cm} factor}{\underbrace{1.602 \times 10^{-19} \hspace{0.1cm} J}}}\\ & = 7.5 \times 10^{6} \hspace{0.1cm} eV = \[ \boxed{7.5 \hspace{0.1cm} MeV}\] \end{aligned}$

$\begin{aligned} V_{a} - V_{b} = \frac{W_{a \rightarrow b}}{q} & = \frac{1.2 \times 10^{-12} \hspace{0.1cm} J}{1.602 \times 10^{-19} \hspace{0.1cm} C} \\ & = 7.5 \times 10^{6} \hspace{0.1cm} J/C = 7.5 \times 10^{6} \hspace{0.1cm} V \\ & = \[ \boxed{7.5 \hspace{0.1cm} MV}\] \end{aligned}$

We can get the same result even more easily by remembering that 1 electron volt is equal to 1 volt multiplied by the charge $e$ . The work done is $7.5 \times 10^{6} \hspace{0.1cm} eV$ and the charge is $e$ so the potential difference is $\left ( 7.5 \times 10^{6} \hspace{0.1cm} eV \right ) / e = 7.5 \times 10^{6} \hspace{0.1cm} V$ .

Example 2: The charges in the figure are fixed in space. Find the value of the distance x so that the electric potential energy of the system is zero.

Solution
To solve this, we simply add up all the potential energies between all pairs of charges, let their sum be 0, and solve for the corresponding $x$ .

Let $l = 14.6 \hspace{0.1cm} cm = .146 \hspace{0.1cm} m$ and $q_{1}$ be the charge located at the left, $q_{2}$ be the charge located in the middle, and $q_{3}$ be the charge located at the right.

$q_{1} = 25.5 \hspace{0.1cm} nC = 2.55 \times 10^{-8} \hspace{0.1cm} C$
$q_{2} = 17.2 \hspace{0.1cm} nC = 1.72 \times 10^{-8} \hspace{0.1cm} C$
$q_{3} = -19.2 \hspace{0.1cm} nC = -1.92 \times 10^{-8} \hspace{0.1cm} C$

Using eq.(6), the sum of the potential energies between all pairs of charges is

$U = \frac{1}{4\pi \epsilon _{0}} \cdot \frac{q_{1}q_{2}}{l} + \frac{1}{4\pi \epsilon _{0}} \cdot \frac{q_{1}q_{3}}{x + l} + \frac{1}{4\pi \epsilon _{0}} \cdot \frac{q_{2}q_{3}}{x}$

Equating to 0,

$\begin{aligned} U & = \frac{1}{4\pi \epsilon _{0}} \cdot \frac{q_{1}q_{2}}{l} + \frac{1}{4\pi \epsilon _{0}} \cdot \frac{q_{1}q_{3}}{x + 1} + \frac{1}{4\pi \epsilon _{0}} \cdot \frac{q_{2}q_{3}}{x} = 0 \\ 0 & = \frac{1}{4\pi \epsilon _{0}} \left [ \frac{q_{1}q_{2}x\left ( x + l \right ) + q_{1}q_{3}lx + q_{2}q_{3}l\left ( x + l \right )}{xl \left ( x + l \right )} \right ]\\ 0 & = \underset{a}{\underbrace{\left ( q_{1} q_{2}\right )}} \hspace{0.1cm} x^{2} + \underset{b}{\underbrace{\left ( q_{1}q_{2} + q_{1}q_{3} + q_{2}q_{3}\right )}}l \hspace{0.1cm} x + \underset{c}{\underbrace{\left ( q_{2}q_{3} \right )}} l^{2} \\ x & = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \hspace{4.5cm} quadratic \hspace{0.1cm} formula \end{aligned}$

Plugging the values for $q_{1}$ , $q_{2}$ , $q_{3}$ and $l$ to solve for the constants $a$ , $b$ , and $c$ , we find that x=0.205 m = 20.5 cm

$x = 0.205 \hspace{0.1cm} m = 20.5 \hspace{0.1cm} cm$

Example 3: A point charge has $q = 1.16 \hspace{0.1cm} \mu C$ . Consider point $A$ , which is $2.06 \hspace{0.1cm} m$ from $q$ and point $B$ , which is $1.17 \hspace{0.1cm} m$ from $q$ , as shown in (a) and (b):

(a) Find the potential difference $V_{A} - V_{B}$ in (a)
(b) Repeat for points $A$ and $B$ located as shown in (b).

Solution: To get the potential difference, we just obtain the electric potential at both $A$ and $B$ , and take the difference. Let the distance of $q$ from $A$ to be $x_{A}$ and the distance of $q$ from $B$ to be $x_{B}$ .

(a) Using eq.(10) to obtain the electric potential at both $A$ and $B$ ,

$\begin{aligned} V_{A} & = \frac{1}{4\pi \epsilon _{0}} \frac{q}{x_{A}} \\ V_{B} & = \frac{1}{4\pi \epsilon _{0}} \frac{q}{x_{B}} \end{aligned}$

Getting the potential difference,

$\begin{aligned} V_{A} - V_{B} & = \frac{q}{4\pi \epsilon _{0}} \left [ \frac{1}{x_{A}} - \frac{1}{x_{B}} \right ] \\ V_{A} - V_{B} & = \left ( 8.988 \times 10^{9} \hspace{0.1cm} N \hspace{0.1cm} m^{2} / C^{2} \right )\left ( 1.16 \times 10^{-6} \hspace{0.1cm} C \right )\left ( \frac{1}{2.06 \hspace{0.1cm} m} - \frac{1}{1.17 \hspace{0.1 cm}m } \right ) \\ V_{A} - V_{B} & \approx - 3,849.9756 \hspace{0.1cm} V \end{aligned}$

$\therefore V_{A} - V_{B} \approx -3.85 \hspace{0.1cm} kV$

(b) Since the distances and everything else in this item are the same as that in (a), the potential difference is still $-3.85 \hspace{0.1cm} kV$ .

In both figures, the point $B$ belongs to the same equipotential surface. An equipotential surface is a three-dimensional surface on which the electric potential $V$ is the same at every point. If a test charge is moved from point to point on such a surface, the electric potential energy remains constant.

Example 4: A solid non-conducting sphere of radius $R$ carries a non-uniform charge distribution with charge density $\rho = \rho _{0}r/R, \rho _{0}$ is a constant and r is the distance from the center of the sphere. Find the potential outside the sphere.

Solution: The first step in solving this problem is finding an expression for the electric field outside the sphere using Gauss’s law. With this information, we can then solve for the electric potential.

To solve for the electric field, we construct a spherical Gaussian surface of radius $r$ such that $r > R$ . To use Gauss’s Law, we need to find the total charge first. Here, we follow the same steps we used in solving for the electric field in the previous tutorial.

We know that the total charge can be expressed as the product of the charge distribution and the total volume of the sphere, or

$Q = \rho V \hspace{0.5cm}\Rightarrow \hspace{0.5cm} dQ = \rho \hspace{0.1cm} dV$

Recall that $\rho = \rho _{0} \frac{r}{R}$ (given) and $V = \frac{4}{3} \pi r^{3}$ (volume of a sphere)

$dV = 4\pi r^{2}dr$

And so,

$\begin{aligned} dQ & = \rho _{0} \frac{r}{R} \cdot 4\pi r^{2} \hspace{0.1cm} dr \\ dQ & = \frac{4\pi \rho _{0} r^{3}}{R} \hspace{0.1cm} dr \end{aligned}$

We integrate both sides, with the right-hand side integrated from 0 to $R$ , which is the radius of the sphere.

$\begin{aligned} Q & = \int_{0}^{R} \frac{4\pi \rho _{0}r^{3}}{R} \hspace{0.1cm} dr = \frac{\pi \rho _{0}r^{4}}{R} \Big|_{r=0}^{r=R} \\ & = \pi R^{3}\rho _{0} \end{aligned}$

The electric field is

$\begin{aligned} \oint \overrightarrow{E} \cdot d \overrightarrow{A} & = \frac{Q_{encl}}{\epsilon _{0}} \\ E \cdot \left ( 4 \pi r^{2} \right ) & = \frac{\pi R^{3}\rho _{0}}{\epsilon _{0}} \\ E & = \frac{\rho _{0}R^{3}}{4\epsilon _{0}r^{2}} \end{aligned}$

We can now solve for the potential using eq. (15). We set that $V = 0$ at $r = \infty$ and at the path taken by any point charge is a radial vector $\hat{r}$ parallel to the direction of the electric field to $r$ . This means that $\overrightarrow{E} \cdot \hat{r} = \left | \overrightarrow{E} \right | = E$ . Doing so:

$\begin{aligned} V & = - \int_{\infty }^{r} \overrightarrow{E} \cdot d \overrightarrow{l}\\ & = - \int_{\infty }^{r} \frac{\rho _{0}R^{3}}{4\epsilon _{0}r^{2}} \hspace{0.1cm} dr = - \frac{\rho _{0}R^{3}}{4\epsilon _{0}} \int_{\infty }^{r} \frac{1}{r^{2}} \hspace{0.1cm} dr \\ & = - \frac{\rho _{0}R^{3}}{4\epsilon _{0}} \left [ - \frac{1}{r} \Big|_{r=\infty }^{r=r} \right ] \\ & = \[ \boxed{\frac{\rho _{0}R^{3}}{4\pi \epsilon _{0}r}}\] \end{aligned}$

Authored By

Susie Maestre

Susie is an Electronics Engineer and is currently studying Microelectronics. She loves fictional novels, motivational books as much as she loves electronics and electrical stuffs. Some of her fields of interests are digital designs, biomedical electronics, semiconductor physics, and photonics.

Next up:

Make a Temperature Logger Using EEPROM and LCD Using MCC | Embedded C Programming - Part 37