Understanding Electric Fields due to various charges
Published
An electric field is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. The electric field is defined at each point in space as the force per unit charge that would be experienced by a test charge if held stationary at that point. As the electric field is defined in terms of force, and force is a vector, it follows that an electric field is a vector field.
 , and let
, and let  be the electric force of A on B. One way to think about this force is as an “action at-a-distance” force—that is, as a force that acts across empty space without needing physical contact between A and B. But a more fruitful way to visualize the repulsion between A and B is as a two-stage process. We first envision that body A, as a result of the charge that it carries, somehow modifies the properties of the space around it. Then body B, as a result of the charge that it carries, senses how space has been modified at its position. The response of body B is to experience the force
be the electric force of A on B. One way to think about this force is as an “action at-a-distance” force—that is, as a force that acts across empty space without needing physical contact between A and B. But a more fruitful way to visualize the repulsion between A and B is as a two-stage process. We first envision that body A, as a result of the charge that it carries, somehow modifies the properties of the space around it. Then body B, as a result of the charge that it carries, senses how space has been modified at its position. The response of body B is to experience the force  .
.
Consider the charged body A by itself. We say that the charged body A causes an electric field at point P (and at all other points in the neighborhood). This electric field is present at P even if there is no charge at P; it is a consequence of the charge on body A only.
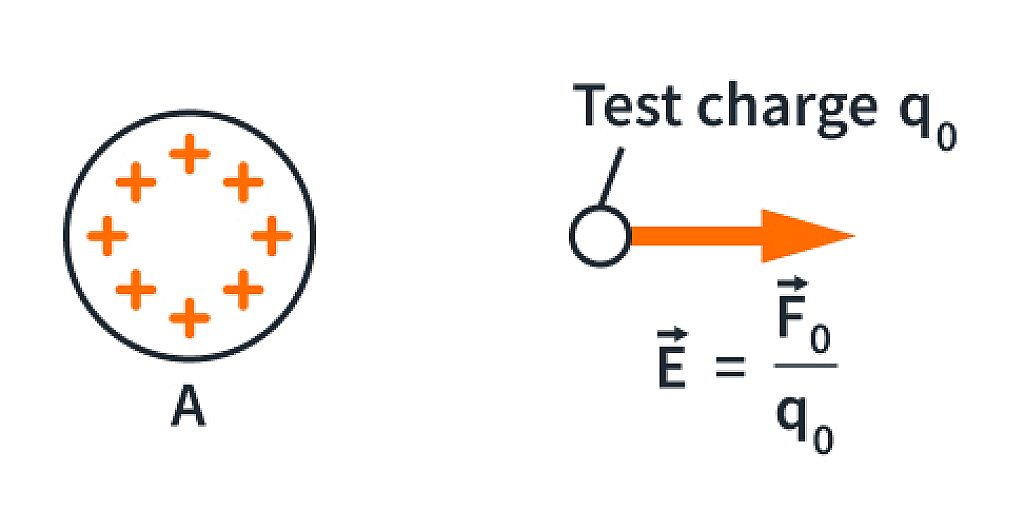
 is then placed at point P, it experiences the force
is then placed at point P, it experiences the force  . We take the point of view that this force is exerted on
. We take the point of view that this force is exerted on  by the field at P. Thus the electric field is the intermediary through which A communicates its presence to
by the field at P. Thus the electric field is the intermediary through which A communicates its presence to  .
.
Because the point charge 




 at a point as the electric force
at a point as the electric force  experienced by a test charge
experienced by a test charge  at the point, divided by the charge
at the point, divided by the charge  . That is, the electric field at a certain point is equal to the electric force per unit charge experienced by a charge at that point:
. That is, the electric field at a certain point is equal to the electric force per unit charge experienced by a charge at that point: at a certain point is known, rearranging the equation gives the force
at a certain point is known, rearranging the equation gives the force  experienced by a point charge
experienced by a point charge  placed at that point:
placed at that point:  (force exerted on a point charge
(force exerted on a point charge  by an electric field
by an electric field  ). The charge
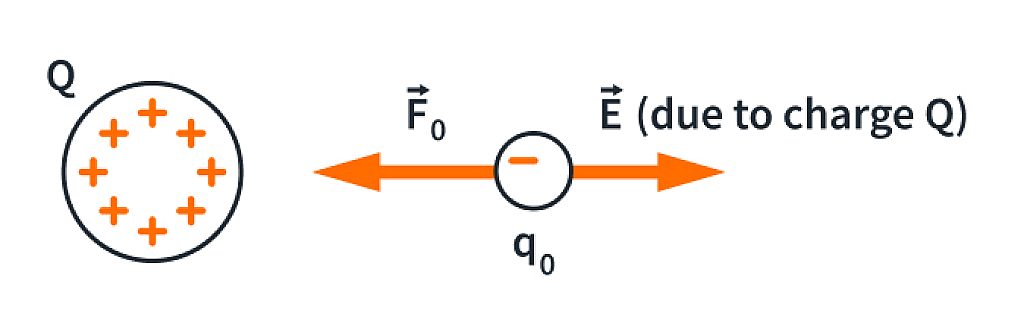
). The charge  can be either positive or negative. If
can be either positive or negative. If  is positive, the force experienced by the charge is in the same direction as
is positive, the force experienced by the charge is in the same direction as  if
if  is negative,
is negative,  and
and  are in opposite directions.
are in opposite directions.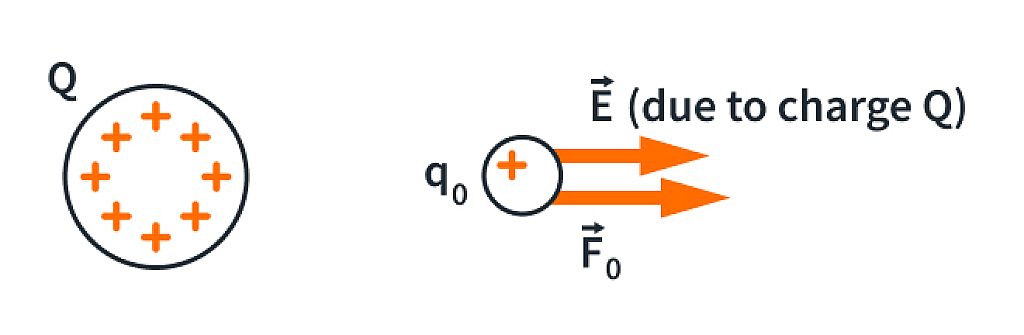
Electric Field of a Point Charge
 , it is easy to find the electric field that it produces. We call the location of the charge the source point, and we call the point P where we are determining the field the field point. If we place a small test charge
, it is easy to find the electric field that it produces. We call the location of the charge the source point, and we call the point P where we are determining the field the field point. If we place a small test charge  at the field point P, at a distance r from the source point, the magnitude
at the field point P, at a distance r from the source point, the magnitude  of the force is given by Coulomb’s law,
of the force is given by Coulomb’s law, the magnitude
the magnitude  of the electric field at P is
of the electric field at P is be a unit vector that points along the line from source point to field point. This unit vector is equal to the displacement vector
be a unit vector that points along the line from source point to field point. This unit vector is equal to the displacement vector  from the source point to the field point, divided by the distance
from the source point to the field point, divided by the distance  between these two points; that is,
between these two points; that is,  . Using the unit vector
. Using the unit vector  , we can write a vector equation that gives both the magnitude and direction of the electric field
, we can write a vector equation that gives both the magnitude and direction of the electric field  :
: is the electric field due to a point charge,
is the electric field due to a point charge,  is the electric constant,
is the electric constant,  is the value of the point charge, and
is the value of the point charge, and  is the distance from the point charge to where the field is measured. By definition, the electric field of a point charge always points away from a positive charge (in the same direction as
is the distance from the point charge to where the field is measured. By definition, the electric field of a point charge always points away from a positive charge (in the same direction as  ) but toward a negative charge (in the direction opposite
) but toward a negative charge (in the direction opposite  ;
;  ).
).
Figure 2: The electric field from an isolated (left) positive charge and (right) negative charge. The field strength is proportional to the density of the lines. The field lines are the paths that a charge would follow as it is forced to move within the field. The field lines are simply representations; the field actually permeates all the space between the lines.
 can vary from point to point, it is not a single vector quantity but rather an infinite set of vector quantities, one associated with each point in space. This is an example of a vector field. If we use a rectangular coordinate system, each component of
can vary from point to point, it is not a single vector quantity but rather an infinite set of vector quantities, one associated with each point in space. This is an example of a vector field. If we use a rectangular coordinate system, each component of  at any point is in general a function of the
at any point is in general a function of the  coordinates of the point.
coordinates of the point.In some situations the magnitude and direction of the field (and hence its vector components) have the same values everywhere throughout a certain region; we then say that the field is uniform in this region. An important example of this is the electric field inside a conductor. If there is an electric field within a conductor, the field exerts a force on every charge in the conductor, giving the free charges a net motion. By definition an electrostatic situation is one in which the charges have no net motion. We conclude that in electrostatics the electric field at every point within the material of a conductor must be zero.
Example: Electric-field magnitude for a point charge
What is the magnitude of the electric field at a field point 3.0 m from a point charge 
Solution. We are given the magnitude of the charge and the distance from the charge to the field point, so we use 

(Coulomb’s constant 
 , it would experience a 5.0 N force. The force on a 2.0-C charge at that point would be
, it would experience a 5.0 N force. The force on a 2.0-C charge at that point would be  , and so on.
, and so on.Example: Electric field vector for a point charge
 is located at the origin. Find the electric field vector at the field point
is located at the origin. Find the electric field vector at the field point  .
.
Solution. We must find the electric-field vector 







 to
to  is
isThe unit vector 
The electric field vector is
 is negative,
is negative,  points from the field point to the charge (the source point), in the direction opposite to
points from the field point to the charge (the source point), in the direction opposite to  (hence the negative
(hence the negative  component). The magnitude of
component). The magnitude of  is
isand the direction in degrees is
Charge Distribution and Superposition of Electric Fields
 At any given point
At any given point  , each point charge produces its own electric field
, each point charge produces its own electric field  , so a test charge
, so a test charge  placed at
placed at  experiences a force
experiences a force  from charge
from charge  , a force
, a force  from charge
from charge  , and so on. From the principle of superposition of forces, the total force
, and so on. From the principle of superposition of forces, the total force  that the charge distribution exerts on
that the charge distribution exerts on  is the vector sum of these individual forces:
is the vector sum of these individual forces: at point
at point  :
:The total electric field at P is the vector sum of the fields at P due to each point charge in the charge distribution. This statement is the principle of superposition of electric fields.
 ). And when charge is distributed through a volume, we use to represent the volume charge density (charge per unit volume,
). And when charge is distributed through a volume, we use to represent the volume charge density (charge per unit volume,  ).
).Example: Uniformly charged rod
 has charge
has charge  uniformly distributed along its length.
uniformly distributed along its length.
(a) What is the linear charge density of the rod?
(b) Find the electric field at point 

(c) If 


Solution.
(a) The linear charge density 
Since the rod is uniformly charged, 
(b) We use 
First, we must obtain an expression for the infinitesimal amount of charge 

Assuming P is at (0,0), we obtain an expression for the electric field by integrating with respect to 


The 

(c) When 



which is the electric field of a point charge.
Charge
 is uniformly distributed around a conducting ring of radius
is uniformly distributed around a conducting ring of radius  . Find the electric field at a point
. Find the electric field at a point  on the ring axis at a distance
on the ring axis at a distance  from its center.
from its center.
Solution. This is a problem in the superposition of electric fields. Each bit of charge around the ring produces an electric field at an arbitrary point on the x-axis; our target variable is the total field at this point due to all such bits of charge.
We divide the ring into infinitesimal segments
 . The linear charge density in this case is
. The linear charge density in this case is 
The ring is uniformly charged, hence 
The charge in a segment of length 
 and another halfway around the ring at
and another halfway around the ring at  . From the superposition of electric force vectors, we see that the net force
. From the superposition of electric force vectors, we see that the net force  these segments exert on a point test charge at
these segments exert on a point test charge at  , and thus their net field
, and thus their net field  , is directed along the x-axis. The same is true for any such pair of opposite segments around the ring, so the net field at
, is directed along the x-axis. The same is true for any such pair of opposite segments around the ring, so the net field at  is along the x-axis:
is along the x-axis:
 , note that the square of the distance
, note that the square of the distance  from a single ring segment to the point
from a single ring segment to the point  is
is  . Hence the magnitude of this segment’s contribution
. Hence the magnitude of this segment’s contribution  to the electric field at is
to the electric field at is . We know
. We know  and the figure shows that
and the figure shows that and
and  ,
,Substituting 
 we integrate this expression over the entire ring, that is from
we integrate this expression over the entire ring, that is from  to
to  . The integrand is constant for all points on the ring, so it can be taken outside the integral. Hence we get
. The integrand is constant for all points on the ring, so it can be taken outside the integral. Hence we getSubstituting 
 at the center of the ring
at the center of the ring  . This makes sense; charges on opposite sides of the ring push in opposite directions on a test charge at the center, and the vector sum of each such pair of forces is zero.
. This makes sense; charges on opposite sides of the ring push in opposite directions on a test charge at the center, and the vector sum of each such pair of forces is zero. is much farther from the ring than the ring’s radius, we have
is much farther from the ring than the ring’s radius, we have  and the denominator becomes
and the denominator becomes  , so
, so  . In this limit the electric field at
. In this limit the electric field at  is
isWhen the ring is so far away that its radius is negligible in comparison to the distance x, its field is the same as that of a point charge.
Example: Uniformly charged disk
 has a uniform positive surface charge density
has a uniform positive surface charge density  . Find the electric field at a point along the axis of the disk a distance x from its center, assuming that
. Find the electric field at a point along the axis of the disk a distance x from its center, assuming that  is positive.
is positive.
We represent the charge distribution as a collection of concentric rings of charge 
 , inner radius
, inner radius  , and outer radius
, and outer radius  . Its area is approximately equal to its width
. Its area is approximately equal to its width  times its circumference
times its circumference  , or
, or . The disk is uniformly charged, hence
. The disk is uniformly charged, hence  is a constant. The charge per unit area is
is a constant. The charge per unit area isso the charge of the ring is
 , we use
, we use  in place of
in place of  in the result of the previous example, and replace the ring radius
in the result of the previous example, and replace the ring radius  with. Then the field component
with. Then the field component  at point
at point  due to this ring is
due to this ring is 
 over
over  through the entire disk, from
through the entire disk, from  to
to  .
.Let 
 ,
,  and when
and when  ,
,  .
.So the integral becomes
In this tutorial we performed quite tedious calculations for the electric field. In the next tutorial, we will discuss Gauss’s Law and apply this general law for the electric field at any point along a closed surface. Gauss’s law allows the evaluation of the amount of enclosed charge by mapping the field on a surface outside the charge distribution. It is an essential tool since it simplifies the calculation of the electric field for geometries of sufficient symmetry.

Get the latest tools and tutorials, fresh from the toaster.







































