Gauss’ Law for Magnetic Fields: Integral Form

Gauss’ Law for Magnetic Fields (GLM) is one of the four fundamental laws of classical electromagnetics, collectively known as Maxwell’s Equations. Before diving in, the reader is strongly encouraged to review Section 2.5. In that section, GLM emerges from the “flux density” interpretation of the magnetic field. GLM is not identified in that section, but now we are ready for an explicit statement:

This is expressed mathematically as follows:

where

is magnetic flux density and

is a closed surface with outward-pointing differential surface normal

. It may be useful to consider the units.

has units of Wb/m²; therefore, integrating

over a surface gives a quantity with units of Wb, which is magnetic flux, as indicated above.

GLM can also be interpreted in terms of magnetic field lines. For the magnetic flux through a closed surface to be zero, every field line entering the volume enclosed by

must also exit this volume – field lines may not begin or end within the volume. The only way this can be true for every possible surface

is if magnetic field lines always form closed loops. This is in fact what we find in practice, as shown in Figure 7.2.1.

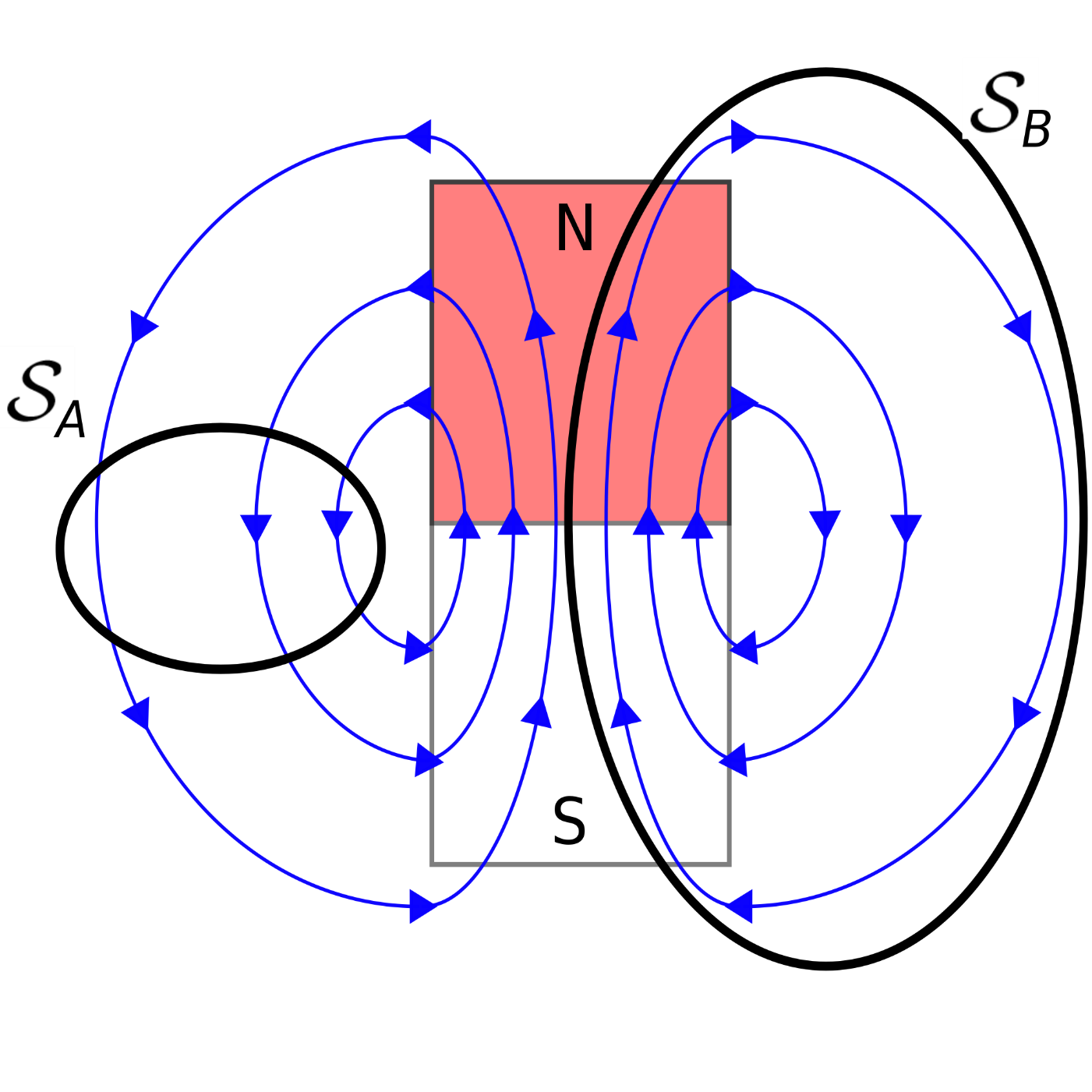
Figure 7.2.1: Gauss’ Law for Magnetostatics applied to a two-dimensional bar magnet. For the surface

, every field line entering

also leaves S, so the flux through

is zero. For the surface

, every field line within

remains in

, so the flux through

is again zero. Image used wtih permission (CC BY SA 4.0).

Following this argument one step further, GLM implies there can be no particular particle or structure that can be the source of the magnetic field (because then that would be a start point for field lines). This is one way in which the magnetic field is very different from the electrostatic field, for which every field line begins at a charged particle. So, when we say that current (for example) is the source of the magnetic field, we mean only that the field coexists with current, and not that the magnetic field is somehow attached to the current. Summarizing, there is no “localizable” quantity, analogous to charge for electric fields, associated with magnetic fields. This is just another way in which magnetic fields are weird!

• “Gauss’ Law for Magnetism” on Wikipedia.
• “Maxwell’s Equations” on Wikipedia.