Introduction to Control Systems 1.1

Control Systems is an interdisciplinary topic involving all different types of engineering and it has applications everywhere, from small electronic circuits to a big industrial robot. Even our own body is a very good example of a control system. How? We shall see!

In this set of tutorial series, we shall start with the basic principles in control systems and gradually work out the control concepts of practical systems through analyzing their responses. I would suggest you learn more about Laplace transforms in the equations menu (Equations - Differential Equations - Laplace) before starting this tutorial series.

In this introductory tutorial, we shall try to understand the concepts involved with control systems so that everything we cover later will make sense.

Before we find out what control systems are, let’s first understand what is meant by a system. A system is a collection of things that are put together with the intention to perform a specific task. When we excite a system with an input, we get a certain response. A resistor, a capacitor, an air conditioner, an automobile are some examples of systems. Sometimes a system is referred to as a “plant.”

A control system is a mechanism that directs the input it receives through the systems and regulates their output.

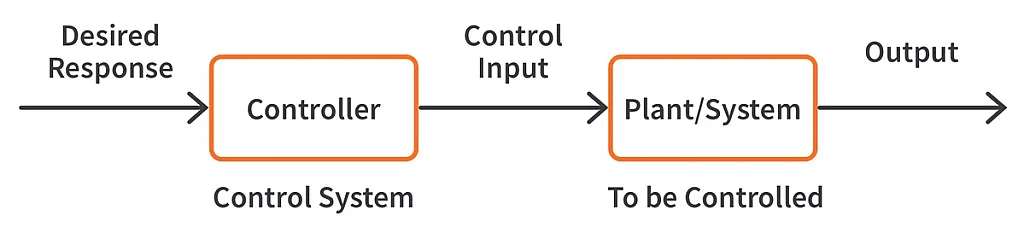
The above figure shows the block diagram of a control system. A control system alters the response of a plant or a system as desired. For example, assume we have a system that will be controlled, let’s say a motor whose position is to be controlled. We employ a servomechanism here, which is the control system (or the controller), which gives a certain control input to the motor on how much to rotate. The end goal is for the entire system (the system and the controller) to perform the desired objective.

Now say we need to cook a potato in a traditional microwave, the process would look like something below:

Now, the potato being cooked depends on a lot of factors like the size of the potato, its freshness, etc. Simply setting a fixed time in the timer doesn’t ensure that the potato is cooked. So, what do we do?

We’ll now add a sensor/an instrument that senses if the potato is cooked. Let’s call it a “cookometer”. This will make the microwave smarter. Now the process should look like something below:

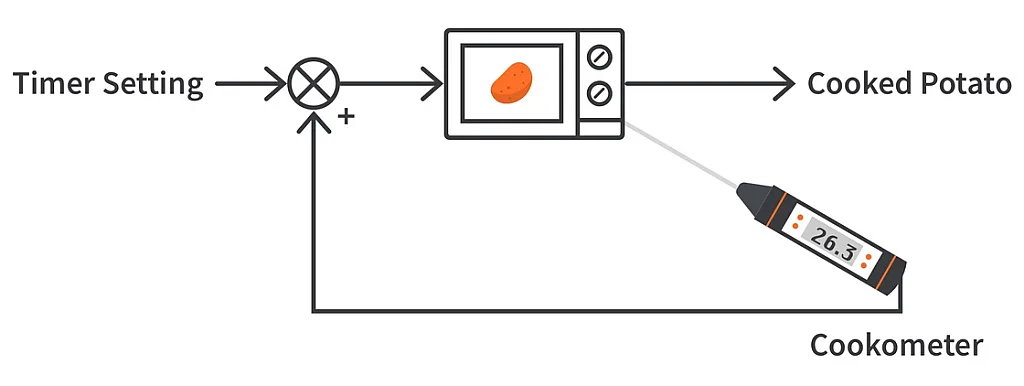
Here, if the potato is not fully cooked, the cookometer will add up extra cooking time and make sure the potato is fully cooked.

The two examples discussed here are the two basic types of control systems. The former is the open loop control system and the latter one is the closed loop control system.

An open loop control system is straightforward. Here, the control action is independent of the fact that we achieved the desired output or not. In short, there is no feedback involved.

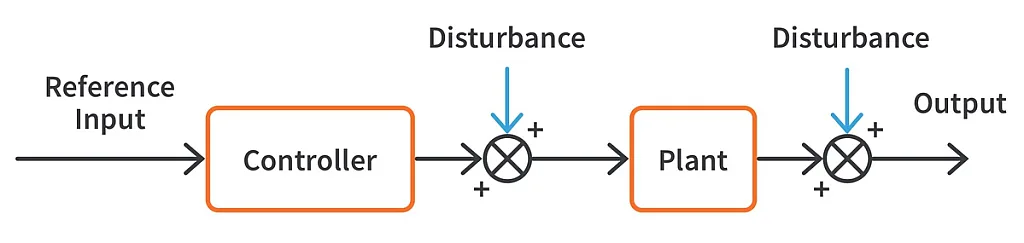
In this case, we have no idea if the desired output is obtained as there could be additional disturbances during the control process. The faithfulness of this type of control system depends greatly on the accuracy of the initial calibration and, hence, are less reliable. In certain cases, where accuracy of the output isn’t an issue, it would be beneficial for us to go with open loop control as it would be a lot cheaper. A good example would be the control of simple traffic lights where the operation of each light depends only on a fixed time.

The closed loop control systems are also known as feedback control systems. Here, the control action is dependent on the desired output. A closed loop control system can have one or more feedback paths.

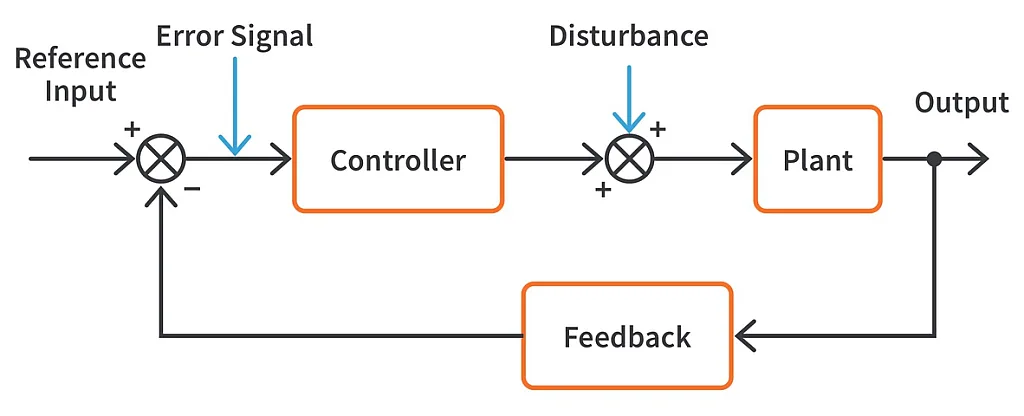
In a closed loop system, the output is compared with the reference input and an error-signal is generated. This error signal is fed to the controller to reduce this error and hence obtain the desired output. This process happens iteratively.

These types of control systems are very reliable and the accuracy of the output is very high. The trade-off is the cost of the system may go up and the system may become complex, but in many cases it is usually worth it.

Feedback is that which differentiates open loop and closed loop systems. It can also be said that feedback is that which turns an open loop control system into a closed loop control system. Feedback feeds a part of the output back to the input by the means of sensors / transducers. This feedback can either be added to the input or subtracted from the input and based on what is done, we categorize feedback into positive feedback and negative feedback. When the feedback is added to the input, it is called positive feedback. Here, the error signal never decreases and hence positive feedback has its application in only a very few areas like signal generators and oscillators. When the feedback is subtracted from the input, it is called a negative feedback. Here, the error signal gradually decreases and the system attains desired output. The majority of the control systems out there are based on negative feedback.

Now, we shall try to understand the effects of using feedback through an Operational amplifier. If you’re not very familiar with op-amps, check out more on operational amplifiers here:

The Open Loop Configuration

The Closed Loop Configuration

Feedback generally reduces the system gain as in this case, the open loop gain of an op amp is very high and hence the output waveform is clipped as it cannot go beyond the supply (12V in this case). With the addition of a feedback resistor, in closed loop configuration, the gain is significantly reduced.

Although feedback reduces system gain, this is not always the case. The system gain increases when we use positive feedback. It also depends on the frequency of operation. Feedback could increase the system gain in one frequency range and decrease it in another frequency range. We shall see more about this in the upcoming chapters.

The output in the case of an open loop system largely depends on the supply levels. The output which was around 10V when the supply was 12V changes to 8V when the supply is changed to 10V. But in the case of the closed loop, it remains nearly the same even though the supply voltage changes. Hence, we can say that the effect of changing parameters of the system can be reduced to a large extent by having feedback.

In this case, having feedback in a system increases its bandwidth. In this situation, bandwidth refers to the range of frequency for which we get our desired output.

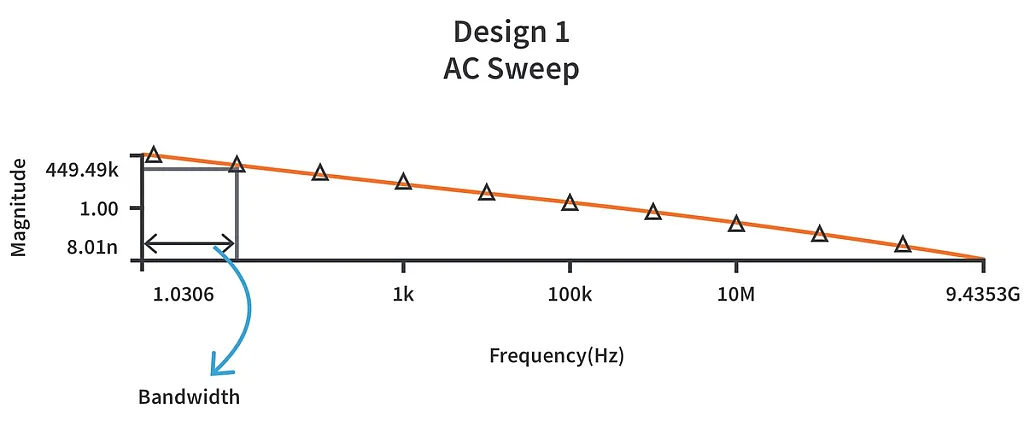
For the open loop configuration, if we look at the frequency response,

For the closed loop configuration,

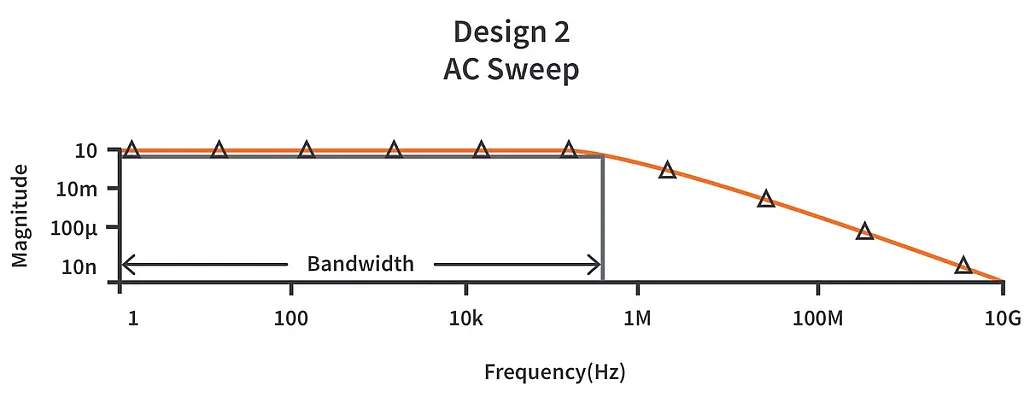
As we can see from the above frequency responses, it is evident that inclusion of feedback increases the bandwidth. It is worth noting here that with positive feedback, the bandwidth decreases.

Let’s consider an open loop system that is originally stable, and then we introduce feedback. This feedback can make the system more stable or completely unstable. It’s like a two-edged sword. In order to improve stability, feedback must be applied properly or else feedback will turn out to be harmful. We shall discuss this in detail in the chapters that will follow but it's good to know that stability needs to be taken into account eventually.

Apart from these, feedback is also known to reduce the system response time. With every cycle of feedback, the output is forced towards the desired output and this will reduce the time the system takes to attain desired output. We will look at this in greater detail when we study time response analysis.

Check this out:

Here, Josh removes the potentiometer from the servomotor. What?? He removed the feedback from a closed loop control system and turned it into an open loop control system. This makes the servomotor less robust now!

Let’s summarize by taking an example of you driving a car. In this case, identify

• The Plant
• The Control System
• Reference Input
• Control Input
• The Output
• Disturbance

Take a moment to think before you proceed reading further.

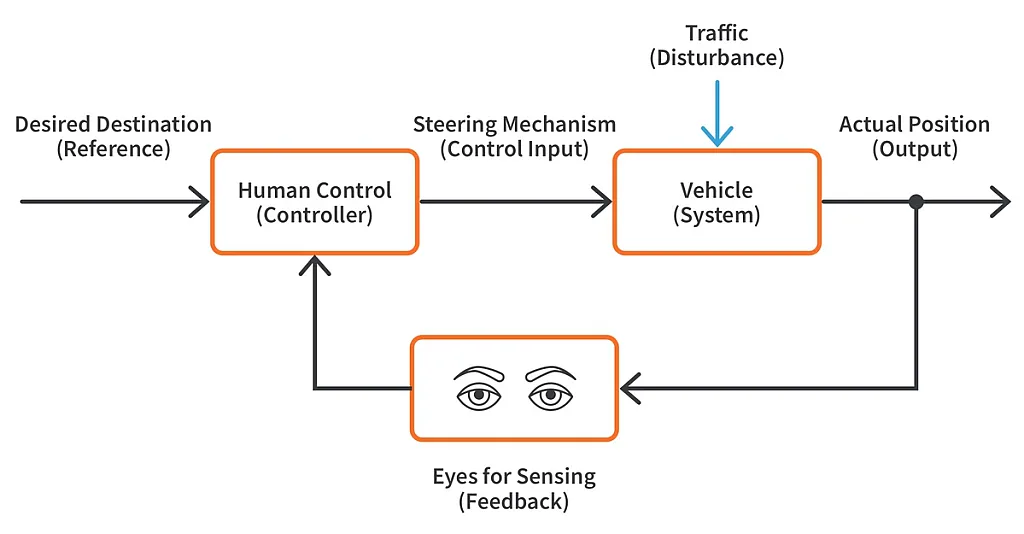
When we drive a car, we want to go from a point A to a point B. So here, point B is the destination. Now, at each point, we see how far we are from point B and then our body itself is the system providing control action. Hence, the reference is the destination, the control input is the steering mechanism which steers our car from point A to point B. the output is the actual position. The disturbance here could be the traffic, road conditions, etc.

In this introductory tutorial, we learnt what a control system means. Feedback in a system is what that distinguishes the closed loop system from the open loop system. We understood how a closed loop control system with feedback gives us our desired output. Feedback impacts a lot of parameters in a system and a few important parameters are its gain, bandwidth, sensitivity to parameter variations, stability and response time.

To get an intuitive understanding of control systems, observe things around you and try to figure out the elements involved in that control system like the example above. In the next section, we shall learn about how to model these systems.

Software used in simulations: NI Multisim