Op-Amp Differentiator

Have you ever wondered how to create an op-amp differentiator? When learning calculus, you learn about differentiation, or derivatives, that mathematically describe the rate of change of a function. For electronics, we are deriving the rate of change of an input voltage in a circuit via an operational amplifier differentiator. In this tutorial, we’ll learn about the circuit diagram of an op-amp differentiator, we’ll try to understand conceptually how an op-amp differentiator works, then we’ll go over how we come up with the standard equation that describes the behavior of an op-amp circuit.

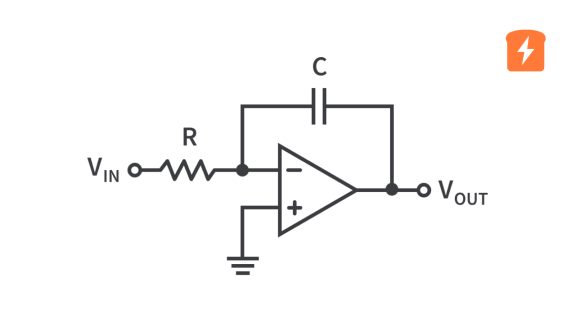
Let’s start by looking at the standard layout of an operational amplifier differentiator circuit.

The standard equation that describes this circuit is:

With this information, you should be able to build and start testing an op-amp on your own but it would be helpful to get into more detail on exactly how the differentiator circuit works and why it behaves the way it does.

As you may remember (if not, we have a tutorial on capacitors here), capacitors block DC signals but pass AC signals. And their impedance is dependent on the frequency of that AC signal - the higher the frequency, the lower the impedance and the easier current passes through the capacitor. Now, keeping that in mind, let’s look again at the circuit.

If the input is a DC signal, that capacitor blocks it completely and V_out doesn’t need to do anything to drive the inverting input to be equal to the non-inverting input. So, any input DC signal will not have any effect on V_out whatsoever. That’s interesting yet useless! Let’s continue.

The magic of the circuit comes into play when V_in is changing. In the time domain, we model the current through a capacitor via the equation:

As the voltage V_in changes, we get a current through the capacitor and that current starts to change the voltage on the inverting input. As the voltage on the inverting input starts to change, the op-amp output immediately changes to both give the current somewhere to flow and also maintain the inverting input at 0V. Specifically, as the input voltage increases, the output decreases, so that current can flow from 0V at the inverting input to the negative voltage at the output. Inversely, as the input voltage decreases, the output increases, so that current that is now flowing backwards, can flow from the output to the inverting input node to the input.

How this creates a differentiation effect is that this response *only* happens as the input voltage is changing - as soon as the input voltage reaches a steady state and current is no longer flowing through the capacitor, the voltage output once again drops to 0.

If you’re in a hurry, you can simply use the standard equation to model the behavior of an operational amplifier differentiator circuit but it’s always good to know how to arrive at the equation yourself. I highly recommend trying to reach that standard equation yourself and then coming back to this to either verify the answer, see a different way of reaching the same answer, or give yourself a clue if you’re struggling.

Here are the steps we follow to derive this equation. If you’re even passingly familiar with KCL, this equation is easy to arrive at, as long as you recall a few important items. First, that the current through a capacitor does not follow Ohm’s law but is described as:

Second, that no current flows in or out of an op-amp’s inputs.

Third, that the op-amp output will drive the inputs so that they are the same voltage.

With those reminders, let’s jump into solving this equation.

Upon inspection, we can see that we can use the node at the inverting input with KCL. The current flowing in and out of the node will be from only two directions. First, the current through the capacitor from one direction and second, out through the resistor in the other and we know that they will be equal to each other. We also know that the voltage at that node is 0 because it’s at a virtual ground due to the non-inverting input being connected directly to ground. Let’s describe that mathematically.

and

Or, in terms of voltage:

And replacing V_- with 0, we get:

And the hard part is done, now it’s some simple algebra that is only hard if you’re prone to making simple mistakes like I am. Let’s get rid of those 0’s first.

Note that we still have the negative on the V_out - I don’t know how many times I’ve seen students drop the negative sign when getting rid of the 0 in front of something. Mainly, those students were me. Don’t be me. Now we can rearrange this to get the final answer.

Voila! Once the original KCL equation is setup, this is very simple. And now you should have a good mathematical understanding of how the output will be the inverted input but scaled by RC.

To help conceptualize, these are a few of the inputs and outputs you could expect from your differentiator. Two things to note here, though. First, the outputs are inverted compared to a simple derivation because, again, the output is both scaled by RC and inverted. Second, while these examples are continuous, you can look at portions of them as discrete events and the associated outputs would still be accurate.

Unlike an integrator circuit, a differentiator circuit doesn’t accumulate error over time, which is quite nice. However, like the integrator circuit or any op-amp circuit, there is only a limited bandwidth within which the circuit has a linear response. As frequency increases too high, the op-amp will not be as responsive and the output will be attenuated.

Another real life consideration is that sometimes the response isn’t as quick or linear as you’d expect mathematically. In particular, with a square wave input, you’d expect very short and steep spikes as the output. In reality, the spikes last longer and aren’t quite as tall as you’d probably expect intuitively. Varying the resistor and capacitor sizes will affect this responsiveness and you can get something that is optimized for your required application.

In this overview, we covered op-amp differentiators, how to make them, how they work conceptually, how their performance is calculated mathematically, as well as showing a few of the typical inputs and outputs used on a differentiator circuit. Finally, we briefly talked about a few of the non-ideal considerations to take into account when working with these in a lab or real-life applications. With that, you should be able to confidently get started with your own work with op-amp differentiator circuits. If you are still confused or have any further questions, you can watch the video tutorial, review this again (there’s no shame in that!), ask a question in the comments below, or jump on and ask in our Discord channel.