Routh-Hurwitz Criterion for Stability Part 1 | Control Systems 3.2
Published
With the background obtained on stability in the previous tutorial, we shall start this tutorial on the Routh-Hurwitz criterion (RH Criterion for short).
First, let’s understand why we need the RH Criterion!
We know that for a system to be stable, its poles should lie in the left half of the s-plane. Seems straight forward, right? For any system, just find the location of the poles by solving the denominator polynomial (also called the characteristic equation) of the transfer function and then if all poles lie in the left half of the s-plane, you call that system stable. Now, you can probably solve a quadratic equation easily. You may also be able to solve a cubic equation with some difficulty. But, as the order of the characteristic equation increases, it gets hard for us to solve and find the location of the poles. Hence, the RH Criterion is where we can determine the stability without solving for the poles.
Before going any further, let’s discuss a few points.
Consider a system with characteristic equation,

For a system to be stable, i.e., to ensure that all the poles lie in the left side of the s-plane, it is necessary that:
- All the coefficients of the equation q(s) should have the same sign,
The main reason why we get a coefficient of a different sign is because of having a pole in the right half plane. Try it out! - There should be no missing term. This means that there should not be any coefficient with zero value between the highest power of s and lowest power of s in the equation q(s).
You might be thinking that if I check for all coefficients and find them all to have the same sign and if none are missing, I can declare the system to be stable. Why would we need something else?
Let’s take an example.
Let q(s) be

The equation has all positive coefficients and there are no missing terms. So, is it stable?
Upon solving, we get the roots of the equation as

Two of the three poles lie in the right half of the s-plane and hence the system is unstable.
As mentioned, these two are just the necessary conditions for a system to be stable. They are not sufficient for one to declare the system stable. In other words, if all the coefficients have the same sign and there are no missing terms, we have no guarantee that the system is going to be stable. But if these conditions are NOT met, we can immediately declare the system unstable. And so this is another need for RH Criterion
With this, let’s start with the Routh-Hurwitz Criterion for stability.
First, this method is both a necessary and a sufficient condition for stability. This method generally has two steps. First is to generate a Routh Array. Next is to interpret the Routh array to find if there are any poles in the right half of the s-plane and determine the stability.
So, let’s generate a Routh Array.
Consider the characteristic equation

First, we shall arrange the coefficients of the equation above in an array in a manner as shown.

As you can see, it is just writing the coefficients alternately in the first and second row of the array starting with the first row.
Next, we shall form the third row with the following procedure. Observe carefully.

Similarly, for the next row we repeat it the same way.
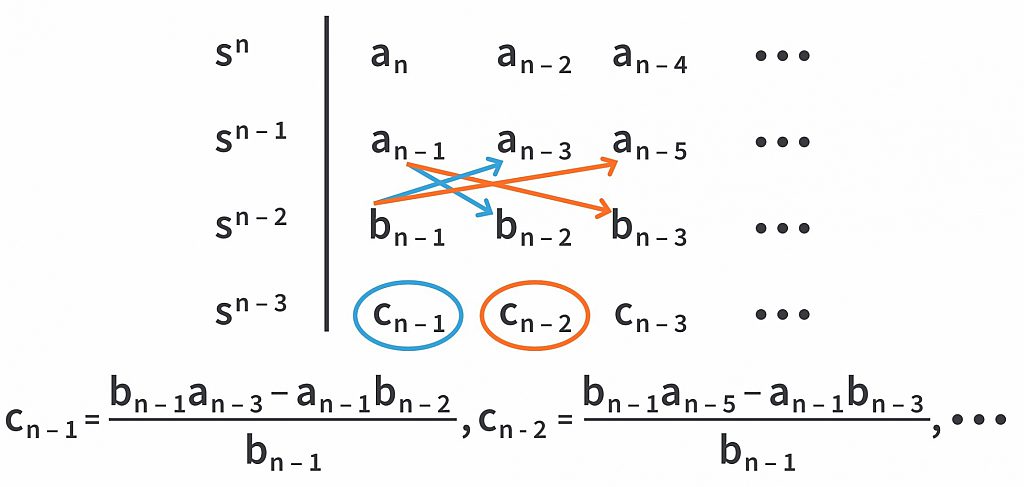
We will continue doing this till s0 and finish generating the complete Routh array as shown

So, now we have the Routh array. This is obviously a tedious task and, with more complicated equations, will be sped up tremendously with some computer logic. However, with this, we shall now understand how we can interpret stability from this array.
As per Routh-Hurwitz criterion, for a system to be stable it is sufficient that all the elements of the first column of the Routh array is positive. If this condition is not met, we can straight away declare the system unstable and the number of sign changes in the first column of the Routh array will give the number of poles that lie in the right half of the s-plane. The illustration below will make it even more clear.

Let’s have an example here.
Consider a system with characteristic equation

The roots of this equation lie at

The system is stable since all the poles lie in the left half of the s-plane.
We shall verify this result with Routh-Hurwitz criterion

Since all the elements of the first column of the routh array are positive, the system is stable.
Now, let’s consider another example.

Since this equation has one negative coefficient, we can straight away say that the system is unstable. But we shall verify the same with Routh-Hurwitz criterion.

Since not all the elements of the first column are positive, the system is unstable and as there is one sign change, there is one pole in the right half of the s-plane.
To summarize, in this tutorial we learned the basic conditions necessary for a system to be stable and then understanding the need for the Routh-Hurwitz criterion. We jumped towards learning the Routh-Hurwitz criterion wherein we first learned to generate a Routh array and then learned how to interpret it.
Take some random characteristic equations and check for their stability. After that, try forming the Routh array for the characteristic equations below


You will get stuck here and will not be able to complete the Routh Array. But don’t worry, the equations above are examples of two special cases which we shall discuss in the next tutorial. We shall also discuss how we can compare the stability of systems using Routh Hurwitz criterion.

Get the latest tools and tutorials, fresh from the toaster.











