Controllers and Compensators | Control Systems 4.1

In the previous tutorial, we understood the root locus plot and how to analyse the stability of a system through it. We now start learning a new chapter which is going to be on controllers and compensators which probably is one of the most important topics in control systems practically. In this tutorial, we shall get hold of the basic task that a controller or a compensator does.

Controllers or compensators are basically systems that operate along with the main plant system to get the desired output from it. But why is it required when we can just design the main system to give us the desired output? It is because when a system is subject to prolonged use (aging), the parameters of the systems can change, and the output and time response specifications then produced may not seem desirable. We should now make changes to the system so that it again gives us the desired response, but that is not always possible. For some systems, once they are designed and developed, it may not be feasible to tweak the system. So, in that case having controllers or compensators having tweakable/tunable parameters along with the main system helps in negating the changes that occur on to the main system due to factors like ageing, external disturbances, etc. The tasks of controllers or compensators can range from maintaining the output within a certain range, decreasing overshoot to decreasing settling time and improving stability. A general block diagram of a controller or compensator along with a closed loop system is shown below.

Before we proceed further, we shall have a quick recap of the time response specifications that we learnt in tutorial 2.4.

A general closed loop second order system is represented by,

The response of this system is described by these time response specifications:

• Rise Time

• Delay Time

• Peak Time

• Percentage Overshoot

• Settling Time

These are pretty much everything that is needed to comment on the performance of a control system. But this is only for a second order system and not all systems we come across in the real world are second order. So, what do we do?

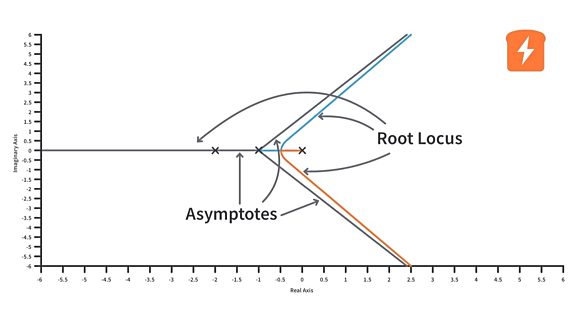
Suppose we have a system of a higher order (more than two poles). Each pole or zero has some contribution to the response of the system and among these, some poles tend to have a much greater influence on the response of the system than the rest. We term such poles as the dominant poles. We then approximate the system by ignoring poles other than the dominant ones and using the same time response specifications as seen previously. The pole zero distribution in the s-plane below shows an example of a higher order system and its dominant poles.

This concept of dominant poles will get clearer as we proceed further on this tutorial, so hold on tight.

Let’s now analyse systems which have an added zero or a pole along with its dominant poles.

Before that, we shall take the transfer function of a series RLC circuit as shown below for this analysis.

For simplicity, if we take R = 1ohm, C = 1F and L = 1H, the transfer function reduces to

Effect of addition of a zero in the left half of s plane:

Let’s add a zero at s = -a.

For that let’s have a transfer function G_c(s),

Now, the response after adding a zero at s = -a becomes,

You might be wondering why is G_c(s) not "s + a" and "1 + s/a", as we can see, both give zero at s = -a. But if you put s = 0, the former expression gives "a" and the latter one gives "1". As we are going to compare the responses, we didn’t want to scale up the response and maintain the DC gain or the zero-frequency gain of the transfer function G_c(s) as 1. In other words, we want the DC gain of G(s) and G₁(s) to be the same. If we put s = 0 in the expressions for G(s) and G₁(s), they both yield the same 1. This ensures us that the responses are of the same scale.

We have taken the values of a to be 0.5, 1, and 10 and simulated it to see its effect on the response of the system using Scilab.

The script for this simulation is as follows,

Let’s look at the response,

What do you infer? Take a while and give it some thought, we shall discuss in some time.

Effect of addition of a zero in the right half of s plane:

Let’s add a zero at s = a.

Just like the previous one, we have

Now, the response after adding a zero at s = -a becomes,

We have taken the values of a to be 0.5, 1, and 10 and simulated it to see its effect on the response of the system using Scilab.

The script for this simulation is as follows,

Let’s look at the response,

Here again, think what you can infer.

Next, we’ll check out the addition of a pole and this will only be to the left half of the s-plane as adding a pole to the right half of the s-plane will make the system unstable.

Effect of addition of a pole in the left half of s plane:

Now, let’s add a pole at s = -a.

For that, we have

The response after adding a zero at s = -a becomes,

We have taken the values of a to be 0.5, 1 and 10 and simulated it to see its effect on the response of the system using Scilab.

The script for this simulation is as follows,

Now, let’s see the response,

So, what do we infer from all these additions of a zero or a pole at various locations?

1. As the value of "a" increases i.e., as the zero of the pole moves away from the imaginary axis, its effect on the response keeps on decreasing. In this analysis, you can see that with a = 0.5, the response is the most affected and with a = 10, the system is least affected.
2. We can also infer that the analysis of systems of higher order becomes easier with the dominant pole concept. The dominant poles mostly exist in conjugate pairs and often, the higher order systems are made that way. To consider a pair of poles as dominant, a general rule that is followed is that the real part of the other poles of the system should be more than five times the real part of the dominant pole pair.
3. By adding a zero or a pole, we can alter the system's response to make it the desired one. For example, if we need to make the response faster, observing the plots, we can tell that adding a zero in the left half of the s-plane would work. Similarly, if we must slow down the system, we can do that by adding a zero in the right half of the s-plane or by adding a pole in the left half of the s-plane, but in the former – we can see an undershoot as seen in the plots. In this way, seeing the requirements, we can add a pole or a zero to the system and tweak its response.

If you can recall, in the previous tutorial, we also had discussed the impact on stability by the addition of a pole or a zero with the help of the root-locus plot.

With this, we can tell that the addition of a pole or a zero has the ability to tweak the system response and as well as to impact the system stability making it the basis of controller design in control systems.

In this tutorial, we started with understanding the need for a controller or a compensator. Then, we discussed the dominant pole concept and how it can be used to approximate the higher order systems. Later, we understood the effect of addition of a zero and a pole at various locations in the s-plane on the system response, familiarizing us with the basic concept behind controller design. In the next tutorial, we shall learn about the proportional control, integral control, derivative control, PI, PD and PID control and also we shall learn how to implement it at a circuit level. Until then, try out adding multiple poles or zeros or both to a transfer function and check the response using Scilab.